Method development for geometric functions pt 2: \(\beta\) parameters with geometric functions.
09/04/20 debugged
26/02/20 v1
Aims:
Develop \(\beta_{L,M}\) formalism.
Develop corresponding numerical methods - see pt 1 notebook.
Analyse geometric terms - see pt 1 notebook.
\(\beta_{L,M}^{MF}\) rewrite
The various terms defined above can be used to redefine the full MF observables, expressed as a set of \(\beta_{L,M}\) coefficients.
The original (full) form for the MF equation, as implemented in ePSproc.mfblm() (note this is defined for an expansion in non-conjugate harmonics, \(Y_{LM}(\theta_{\hat{k}},\phi_{\hat{k}})\)):
Where \(I_{l,m,\mu}^{p_{i}\mu_{i},p_{f}\mu_{f}}(E)\) are the energy-dependent dipole matrix elements.
Substituting the terms above (plus some tidying up with phases etc. - see other notes for full derivation):
And can also reorder…
Add additional (function) labels to track QNs:
Cf. R&U rotational wavepacket case, see also Chpt. 12 in Quantum Met book for similar formalism separating geometric channels:
For details on each term in the tensor product, see the pt 1 notebook. Here we’ll look at the overall result, check for consistency and benchmark.
Setup
[1]:
# Imports
import numpy as np
import pandas as pd
import xarray as xr
# Special functions
# from scipy.special import sph_harm
import spherical_functions as sf
import quaternion
# Performance & benchmarking libraries
# from joblib import Memory
# import xyzpy as xyz
import numba as nb
# Timings with ttictoc or time
# https://github.com/hector-sab/ttictoc
from ttictoc import TicToc
import time
# Package fns.
# For module testing, include path to module here
import sys
import os
modPath = r'D:\code\github\ePSproc' # Win test machine
# modPath = r'/home/femtolab/github/ePSproc/' # Linux test machine
sys.path.append(modPath)
import epsproc as ep
# TODO: tidy this up!
# from epsproc.util import matEleSelector
# from epsproc.geomFunc import geomCalc
* pyevtk not found, VTK export not available.
[2]:
# Load data from modPath\data
dataPath = os.path.join(modPath, 'data', 'photoionization')
dataFile = os.path.join(dataPath, 'n2_3sg_0.1-50.1eV_A2.inp.out') # Set for sample N2 data for testing
# Scan data file
dataSet = ep.readMatEle(fileIn = dataFile)
dataXS = ep.readMatEle(fileIn = dataFile, recordType = 'CrossSection') # XS info currently not set in NO2 sample file.
*** ePSproc readMatEle(): scanning files for DumpIdy segments.
*** Scanning file(s)
['D:\\code\\github\\ePSproc\\data\\photoionization\\n2_3sg_0.1-50.1eV_A2.inp.out']
*** Reading ePS output file: D:\code\github\ePSproc\data\photoionization\n2_3sg_0.1-50.1eV_A2.inp.out
Expecting 51 energy points.
Expecting 2 symmetries.
Scanning CrossSection segments.
Expecting 102 DumpIdy segments.
Found 102 dumpIdy segments (sets of matrix elements).
Processing segments to Xarrays...
Processed 102 sets of DumpIdy file segments, (0 blank)
*** ePSproc readMatEle(): scanning files for CrossSection segments.
*** Scanning file(s)
['D:\\code\\github\\ePSproc\\data\\photoionization\\n2_3sg_0.1-50.1eV_A2.inp.out']
*** Reading ePS output file: D:\code\github\ePSproc\data\photoionization\n2_3sg_0.1-50.1eV_A2.inp.out
Expecting 51 energy points.
Expecting 2 symmetries.
Scanning CrossSection segments.
Expecting 3 CrossSection segments.
Found 3 CrossSection segments (sets of results).
Processed 3 sets of CrossSection file segments, (0 blank)
[3]:
# Tabulate & plot matrix elements vs. Eke
selDims = {'it':1, 'Type':'L'}
matE = dataSet[0].sel(selDims) # Set for N2 case, length-gauge results only.
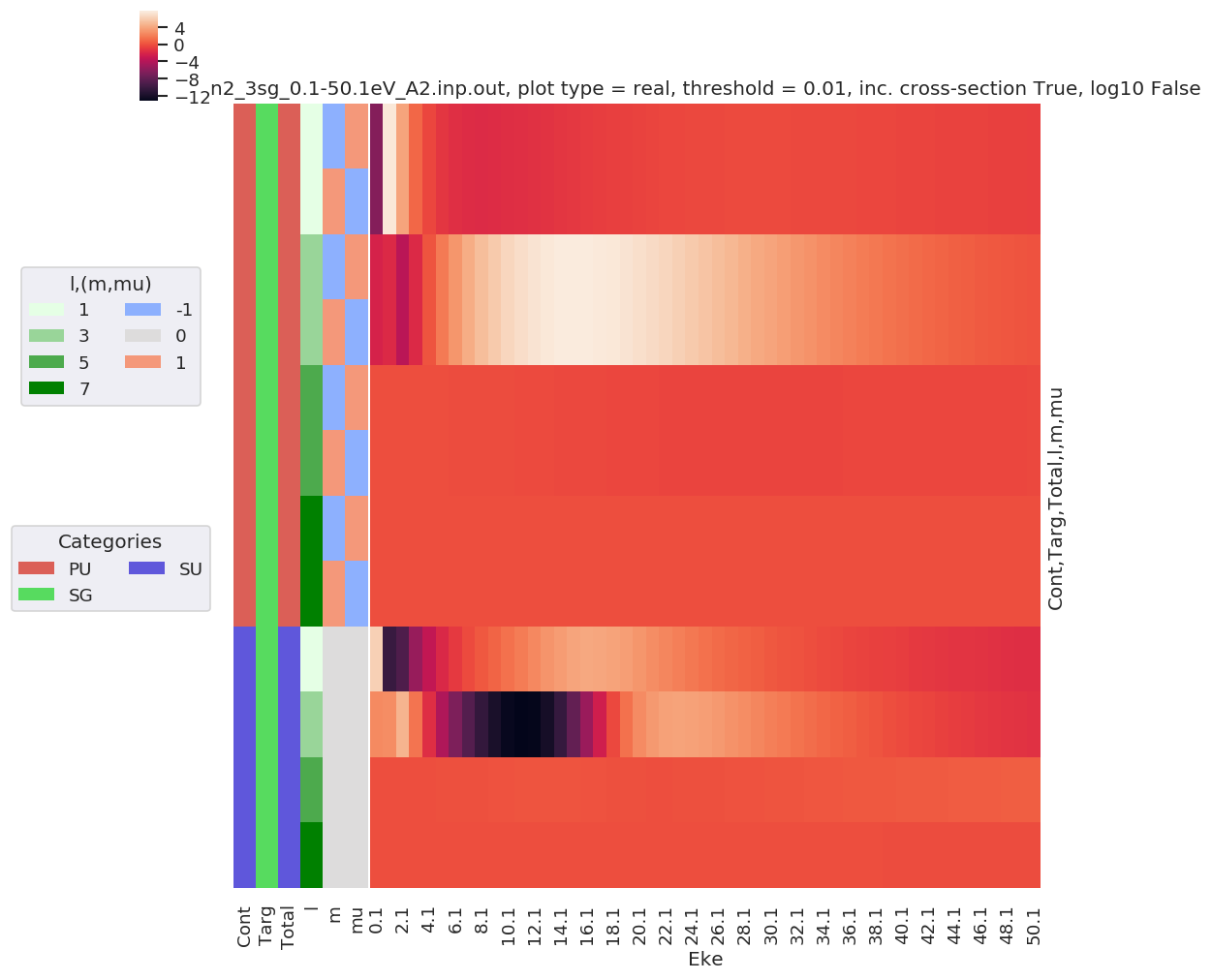
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(matE, xDim = 'Eke', pType = 'r', fillna = True)
daPlotpd
Plotting data n2_3sg_0.1-50.1eV_A2.inp.out, pType=r, thres=0.01, with Seaborn
[3]:
| Eke | 0.1 | 1.1 | 2.1 | 3.1 | 4.1 | 5.1 | 6.1 | 7.1 | 8.1 | 9.1 | ... | 41.1 | 42.1 | 43.1 | 44.1 | 45.1 | 46.1 | 47.1 | 48.1 | 49.1 | 50.1 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cont | Targ | Total | l | m | mu | |||||||||||||||||||||
| PU | SG | PU | 1 | -1 | 1 | -6.203556 | 7.496908 | 3.926892 | 1.071093 | -0.335132 | -1.043391 | -1.396885 | -1.554984 | -1.598812 | -1.573327 | ... | -0.396306 | -0.422225 | -0.448003 | -0.473466 | -0.498463 | -0.522867 | -0.546573 | -0.569493 | -0.591558 | -0.612712 |
| 1 | -1 | -6.203556 | 7.496908 | 3.926892 | 1.071093 | -0.335132 | -1.043391 | -1.396885 | -1.554984 | -1.598812 | -1.573327 | ... | -0.396306 | -0.422225 | -0.448003 | -0.473466 | -0.498463 | -0.522867 | -0.546573 | -0.569493 | -0.591558 | -0.612712 | ||||
| 3 | -1 | 1 | -2.090641 | -1.723467 | -3.571018 | -1.703191 | 0.232612 | 1.862713 | 3.201022 | 4.298839 | 5.198215 | 5.929303 | ... | 1.200463 | 1.040074 | 0.892501 | 0.757189 | 0.633556 | 0.521004 | 0.418928 | 0.326726 | 0.243800 | 0.169566 | |||
| 1 | -1 | -2.090641 | -1.723467 | -3.571018 | -1.703191 | 0.232612 | 1.862713 | 3.201022 | 4.298839 | 5.198215 | 5.929303 | ... | 1.200463 | 1.040074 | 0.892501 | 0.757189 | 0.633556 | 0.521004 | 0.418928 | 0.326726 | 0.243800 | 0.169566 | ||||
| 5 | -1 | 1 | 0.000000 | 0.013246 | 0.000000 | -0.013096 | -0.024367 | -0.033455 | -0.042762 | -0.053765 | -0.067354 | -0.083946 | ... | -0.325544 | -0.318791 | -0.312332 | -0.306211 | -0.300456 | -0.295091 | -0.290130 | -0.285584 | -0.281453 | -0.277737 | |||
| 1 | -1 | 0.000000 | 0.013246 | 0.000000 | -0.013096 | -0.024367 | -0.033455 | -0.042762 | -0.053765 | -0.067354 | -0.083946 | ... | -0.325544 | -0.318791 | -0.312332 | -0.306211 | -0.300456 | -0.295091 | -0.290130 | -0.285584 | -0.281453 | -0.277737 | ||||
| 7 | -1 | 1 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.027469 | 0.028083 | 0.028678 | 0.029257 | 0.029823 | 0.030377 | 0.030923 | 0.031461 | 0.031994 | 0.032523 | |||
| 1 | -1 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.027469 | 0.028083 | 0.028678 | 0.029257 | 0.029823 | 0.030377 | 0.030923 | 0.031461 | 0.031994 | 0.032523 | ||||
| SU | SG | SU | 1 | 0 | 0 | 6.246520 | -10.081763 | -8.912214 | -5.342049 | -3.160539 | -1.795783 | -0.867993 | -0.174154 | 0.400643 | 0.926420 | ... | -0.854886 | -0.940017 | -1.021577 | -1.099776 | -1.174787 | -1.246759 | -1.315814 | -1.382058 | -1.445582 | -1.506467 |
| 3 | 0 | 0 | 2.605768 | 2.775108 | 4.733473 | 1.677812 | -1.450830 | -4.187395 | -6.554491 | -8.601759 | -10.343109 | -11.747922 | ... | -0.293053 | -0.441416 | -0.579578 | -0.708075 | -0.827415 | -0.938075 | -1.040506 | -1.135134 | -1.222361 | -1.302566 | |||
| 5 | 0 | 0 | 0.000000 | -0.020864 | 0.000000 | 0.024263 | 0.042694 | 0.059142 | 0.077308 | 0.099330 | 0.126227 | 0.157745 | ... | 0.490499 | 0.511546 | 0.531810 | 0.551281 | 0.569951 | 0.587815 | 0.604868 | 0.621107 | 0.636528 | 0.651132 | |||
| 7 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | -0.039566 | -0.041422 | -0.043265 | -0.045092 | -0.046901 | -0.048689 | -0.050453 | -0.052190 | -0.053899 | -0.055577 |
12 rows × 51 columns
Numerics
The tensor product is currenty implemented in mfblmXprod, making use of direct multiplication of Xarrays corresponding to each term in the eqns. (As of mid-March 2020, it still needs a bit of work, but is basically working.) See pt 1 for more details of the component tensors.
This is easy to follow, and relatively fast, although can be RAM heavy for large sets of matrix elements (despite the relatively sparse arrays). Parallelization is not yet implemented, but should be fairly easy using Xarray’s GroupBy functionality. Fast functions are used on the back-end, although there is likely some significant speed-ups to be had by making use of GPU methods here (and in the tensor handling) - this will be necessary for larger problems, e.g. fitting data.
Note - quite a bit of the processing is currently due to slow selection/thresholding routines, so there is also some improvements to be made there.
Timing benchmarks are from an AMD Threadripper 1950X workstation (single core only).
Without symmetry summation
Treat continua separately.
[4]:
phaseConvention = 'E' # Set phase conventions used in the numerics - for ePolyScat matrix elements, set to 'E', to match defns. above.
symSum = False # Sum over symmetry groups, or keep separate?
SFflag = True # Include scaling factor to Mb in calculation?
thres = 1e-4
RX = ep.setPolGeoms() # Set default pol geoms (z,x,y), or will be set by mfblmXprod() defaults
start = time.time()
mTermST, mTermS, mTermTest = ep.geomFunc.mfblmXprod(dataSet[0], QNs = None, thres = thres, selDims = {'it':1, 'Type':'L'}, thresDims='Eke', RX=RX, symSum=symSum, SFflag=True, phaseConvention=phaseConvention)
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points, {2} polarizations, threshold={3}.'.format((end-start), mTermST.Eke.size, RX.size, thres))
# Elapsed time = 3.3885273933410645 seconds, for 51 energy points, 3 polarizations, threshold=0.01.
# Elapsed time = 5.059587478637695 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
Elapsed time = 5.240962028503418 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
[5]:
# Full results (before summation)
mTermST.attrs['dataType'] = 'matE' # Set matE here to allow for correct plotting of sym dims.
plotDimsRed = ['Labels','L','M'] # Set plotDims to fix dim ordering in plot
if not symSum:
plotDimsRed.extend(['Cont','Targ','Total'])
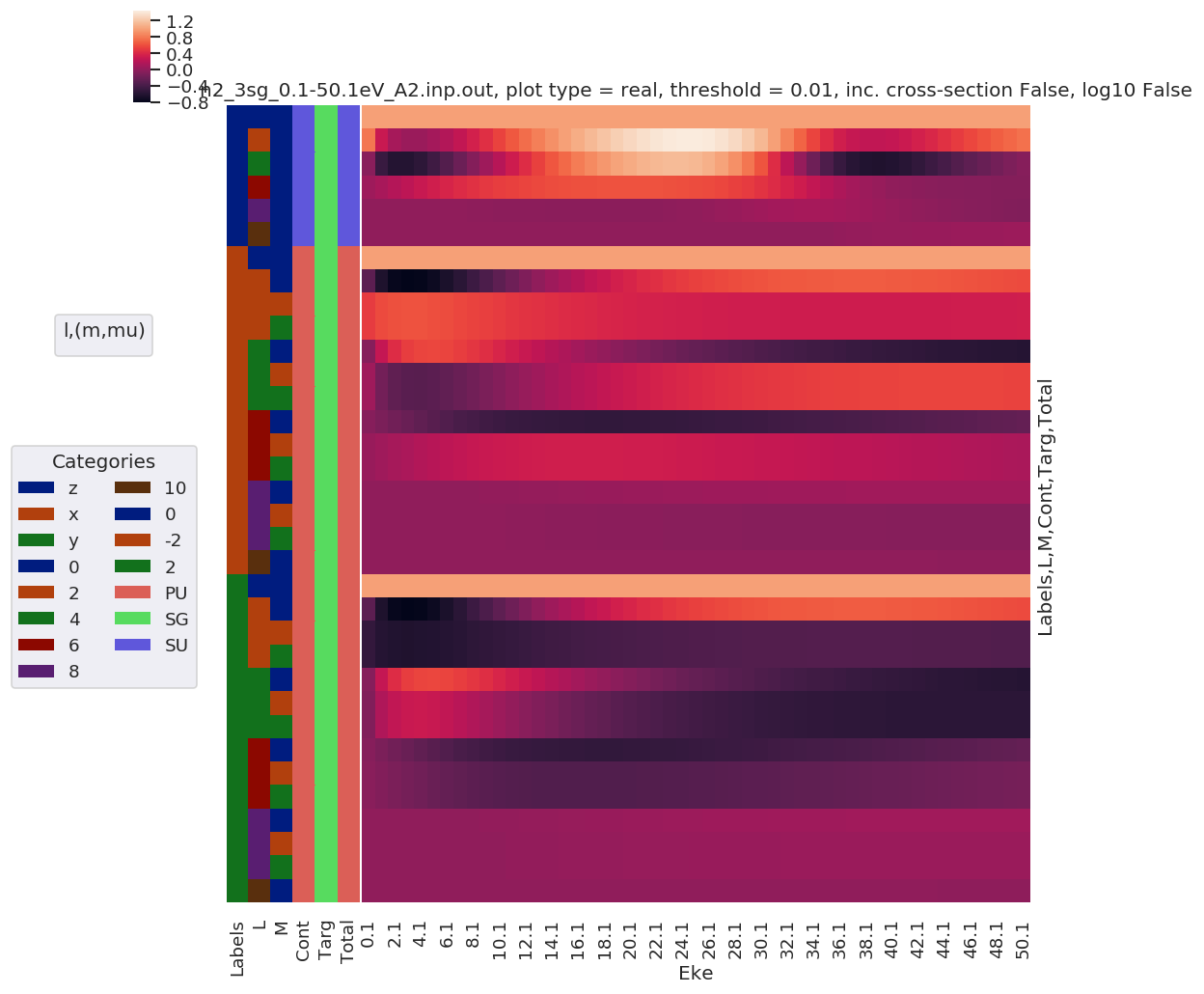
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, plotDims=plotDimsRed, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True, SFflag=False)
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True) # If plotDims is not passed use default ordering.
Plotting data n2_3sg_0.1-50.1eV_A2.inp.out, pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[6]:
# Tabulate complex values...
mTermSTpd, _ = ep.util.multiDimXrToPD(mTermST, colDims='Eke', thres = thres)
mTermSTpd
[6]:
| Eke | 0.1 | 1.1 | 2.1 | 3.1 | 4.1 | 5.1 | 6.1 | 7.1 | 8.1 | 9.1 | ... | 41.1 | 42.1 | 43.1 | 44.1 | 45.1 | 46.1 | 47.1 | 48.1 | 49.1 | 50.1 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cont | L | Labels | M | Targ | Total | |||||||||||||||||||||
| PU | 0 | x | 0 | SG | PU | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | ... | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j |
| y | 0 | SG | PU | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | ... | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | ||
| 2 | x | 0 | SG | PU | -0.272711-0.000000j | -0.638474-0.000000j | -0.775003-0.000000j | -0.814436-0.000000j | -0.794373+0.000000j | -0.736632+0.000000j | -0.655845-0.000000j | -0.562321-0.000000j | -0.463340-0.000000j | -0.363902-0.000000j | ... | 0.655141+0.000000j | 0.650741+0.000000j | 0.645402-0.000000j | 0.639166-0.000000j | 0.632075-0.000000j | 0.624163+0.000000j | 0.615465+0.000000j | 0.606012+0.000000j | 0.595832+0.000000j | 0.584952+0.000000j | |
| -2 | SG | PU | 0.512102-0.000000j | 0.586763+0.000000j | 0.614632-0.000000j | 0.622681-0.000000j | 0.618586-0.000000j | 0.606800-0.000000j | 0.590309-0.000000j | 0.571219+0.000000j | 0.551014+0.000000j | 0.530717-0.000000j | ... | 0.322705+0.000000j | 0.323603+0.000000j | 0.324693-0.000000j | 0.325966-0.000000j | 0.327414+0.000000j | 0.329029+0.000000j | 0.330804+0.000000j | 0.332734+0.000000j | 0.334812+0.000000j | 0.337033+0.000000j | |||
| 2 | SG | PU | 0.512102-0.000000j | 0.586763+0.000000j | 0.614632-0.000000j | 0.622681-0.000000j | 0.618586-0.000000j | 0.606800-0.000000j | 0.590309-0.000000j | 0.571219+0.000000j | 0.551014+0.000000j | 0.530717-0.000000j | ... | 0.322705+0.000000j | 0.323603+0.000000j | 0.324693-0.000000j | 0.325966-0.000000j | 0.327414+0.000000j | 0.329029+0.000000j | 0.330804+0.000000j | 0.332734+0.000000j | 0.334812+0.000000j | 0.337033+0.000000j | |||
| y | 0 | SG | PU | -0.272711+0.000000j | -0.638474-0.000000j | -0.775003-0.000000j | -0.814436-0.000000j | -0.794373+0.000000j | -0.736632-0.000000j | -0.655845-0.000000j | -0.562321-0.000000j | -0.463340-0.000000j | -0.363902-0.000000j | ... | 0.655141+0.000000j | 0.650741-0.000000j | 0.645402+0.000000j | 0.639166+0.000000j | 0.632075+0.000000j | 0.624163+0.000000j | 0.615465+0.000000j | 0.606012-0.000000j | 0.595832-0.000000j | 0.584952+0.000000j | ||
| -2 | SG | PU | -0.512102+0.000000j | -0.586763+0.000000j | -0.614632+0.000000j | -0.622681+0.000000j | -0.618586+0.000000j | -0.606800+0.000000j | -0.590309+0.000000j | -0.571219+0.000000j | -0.551014+0.000000j | -0.530717+0.000000j | ... | -0.322705+0.000000j | -0.323603+0.000000j | -0.324693+0.000000j | -0.325966+0.000000j | -0.327414+0.000000j | -0.329029+0.000000j | -0.330804+0.000000j | -0.332734+0.000000j | -0.334812+0.000000j | -0.337033+0.000000j | |||
| 2 | SG | PU | -0.512102-0.000000j | -0.586763-0.000000j | -0.614632-0.000000j | -0.622681-0.000000j | -0.618586-0.000000j | -0.606800-0.000000j | -0.590309-0.000000j | -0.571219-0.000000j | -0.551014-0.000000j | -0.530717-0.000000j | ... | -0.322705-0.000000j | -0.323603-0.000000j | -0.324693-0.000000j | -0.325966-0.000000j | -0.327414-0.000000j | -0.329029-0.000000j | -0.330804-0.000000j | -0.332734-0.000000j | -0.334812-0.000000j | -0.337033-0.000000j | |||
| 4 | x | 0 | SG | PU | -0.059474-0.000000j | 0.271217+0.000000j | 0.432955-0.000000j | 0.521218-0.000000j | 0.562256-0.000000j | 0.570921-0.000000j | 0.557098-0.000000j | 0.527855+0.000000j | 0.488402+0.000000j | 0.442583-0.000000j | ... | -0.522724+0.000000j | -0.532915+0.000000j | -0.542405+0.000000j | -0.551224+0.000000j | -0.559398+0.000000j | -0.566951-0.000000j | -0.573903-0.000000j | -0.580274-0.000000j | -0.586083+0.000000j | -0.591343+0.000000j | |
| -2 | SG | PU | 0.080503-0.000000j | -0.153387-0.000000j | -0.252803-0.000000j | -0.294656-0.000000j | -0.300540-0.000000j | -0.282866+0.000000j | -0.249932-0.000000j | -0.207619-0.000000j | -0.160148-0.000000j | -0.110502-0.000000j | ... | 0.555041+0.000000j | 0.556708+0.000000j | 0.557821-0.000000j | 0.558406+0.000000j | 0.558483+0.000000j | 0.558074+0.000000j | 0.557198-0.000000j | 0.555870+0.000000j | 0.554108+0.000000j | 0.551925+0.000000j | |||
| 2 | SG | PU | 0.080503-0.000000j | -0.153387-0.000000j | -0.252803-0.000000j | -0.294656-0.000000j | -0.300540-0.000000j | -0.282866+0.000000j | -0.249932-0.000000j | -0.207619-0.000000j | -0.160148-0.000000j | -0.110502-0.000000j | ... | 0.555041+0.000000j | 0.556708+0.000000j | 0.557821-0.000000j | 0.558406+0.000000j | 0.558483+0.000000j | 0.558074+0.000000j | 0.557198-0.000000j | 0.555870+0.000000j | 0.554108+0.000000j | 0.551925+0.000000j | |||
| y | 0 | SG | PU | -0.059474-0.000000j | 0.271217+0.000000j | 0.432955+0.000000j | 0.521218-0.000000j | 0.562256-0.000000j | 0.570921-0.000000j | 0.557098+0.000000j | 0.527855-0.000000j | 0.488402-0.000000j | 0.442583-0.000000j | ... | -0.522724+0.000000j | -0.532915+0.000000j | -0.542405-0.000000j | -0.551224+0.000000j | -0.559398+0.000000j | -0.566951-0.000000j | -0.573903-0.000000j | -0.580274-0.000000j | -0.586083+0.000000j | -0.591343+0.000000j | ||
| -2 | SG | PU | -0.080503+0.000000j | 0.153387-0.000000j | 0.252803-0.000000j | 0.294656-0.000000j | 0.300540-0.000000j | 0.282866-0.000000j | 0.249932-0.000000j | 0.207619-0.000000j | 0.160148-0.000000j | 0.110502-0.000000j | ... | -0.555041+0.000000j | -0.556708+0.000000j | -0.557821+0.000000j | -0.558406+0.000000j | -0.558483+0.000000j | -0.558074+0.000000j | -0.557198+0.000000j | -0.555870+0.000000j | -0.554108+0.000000j | -0.551925+0.000000j | |||
| 2 | SG | PU | -0.080503+0.000000j | 0.153387+0.000000j | 0.252803+0.000000j | 0.294656+0.000000j | 0.300540+0.000000j | 0.282866+0.000000j | 0.249932+0.000000j | 0.207619+0.000000j | 0.160148+0.000000j | 0.110502+0.000000j | ... | -0.555041-0.000000j | -0.556708-0.000000j | -0.557821-0.000000j | -0.558406-0.000000j | -0.558483-0.000000j | -0.558074-0.000000j | -0.557198-0.000000j | -0.555870-0.000000j | -0.554108-0.000000j | -0.551925-0.000000j | |||
| 6 | x | 0 | SG | PU | -0.058944+0.000000j | -0.107815-0.000000j | -0.158159+0.000000j | -0.207754-0.000000j | -0.255279-0.000000j | -0.299612+0.000000j | -0.339916-0.000000j | -0.375688-0.000000j | -0.406740-0.000000j | -0.433136-0.000000j | ... | -0.334833+0.000000j | -0.323955+0.000000j | -0.312985+0.000000j | -0.301929+0.000000j | -0.290790+0.000000j | -0.279573+0.000000j | -0.268281+0.000000j | -0.256919+0.000000j | -0.245491-0.000000j | -0.234000+0.000000j | |
| -2 | SG | PU | 0.040201-0.000000j | 0.073410+0.000000j | 0.107661+0.000000j | 0.141347-0.000000j | 0.173516-0.000000j | 0.203384-0.000000j | 0.230377-0.000000j | 0.254147+0.000000j | 0.274568+0.000000j | 0.291696-0.000000j | ... | 0.201422+0.000000j | 0.193886+0.000000j | 0.186317-0.000000j | 0.178717-0.000000j | 0.171088+0.000000j | 0.163434+0.000000j | 0.155756+0.000000j | 0.148057+0.000000j | 0.140340-0.000000j | 0.132606+0.000000j | |||
| 2 | SG | PU | 0.040201-0.000000j | 0.073410+0.000000j | 0.107661+0.000000j | 0.141347-0.000000j | 0.173516-0.000000j | 0.203384-0.000000j | 0.230377-0.000000j | 0.254147+0.000000j | 0.274568+0.000000j | 0.291696-0.000000j | ... | 0.201422+0.000000j | 0.193886+0.000000j | 0.186317-0.000000j | 0.178717+0.000000j | 0.171088+0.000000j | 0.163434+0.000000j | 0.155756+0.000000j | 0.148057+0.000000j | 0.140340-0.000000j | 0.132606+0.000000j | |||
| y | 0 | SG | PU | -0.058944+0.000000j | -0.107815-0.000000j | -0.158159-0.000000j | -0.207754+0.000000j | -0.255279-0.000000j | -0.299612+0.000000j | -0.339916+0.000000j | -0.375688-0.000000j | -0.406740-0.000000j | -0.433136-0.000000j | ... | -0.334833+0.000000j | -0.323955+0.000000j | -0.312985+0.000000j | -0.301929+0.000000j | -0.290790+0.000000j | -0.279573-0.000000j | -0.268281-0.000000j | -0.256919+0.000000j | -0.245491+0.000000j | -0.234000+0.000000j | ||
| -2 | SG | PU | -0.040201+0.000000j | -0.073410+0.000000j | -0.107661+0.000000j | -0.141347+0.000000j | -0.173516+0.000000j | -0.203384+0.000000j | -0.230377-0.000000j | -0.254147+0.000000j | -0.274568+0.000000j | -0.291696+0.000000j | ... | -0.201422+0.000000j | -0.193886+0.000000j | -0.186317+0.000000j | -0.178717+0.000000j | -0.171088+0.000000j | -0.163434+0.000000j | -0.155756+0.000000j | -0.148057+0.000000j | -0.140340+0.000000j | -0.132606+0.000000j | |||
| 2 | SG | PU | -0.040201-0.000000j | -0.073410-0.000000j | -0.107661-0.000000j | -0.141347-0.000000j | -0.173516-0.000000j | -0.203384-0.000000j | -0.230377-0.000000j | -0.254147-0.000000j | -0.274568-0.000000j | -0.291696-0.000000j | ... | -0.201422-0.000000j | -0.193886-0.000000j | -0.186317-0.000000j | -0.178717-0.000000j | -0.171088-0.000000j | -0.163434-0.000000j | -0.155756-0.000000j | -0.148057-0.000000j | -0.140340-0.000000j | -0.132606-0.000000j | |||
| 8 | x | 0 | SG | PU | 0.000181-0.000000j | 0.000676+0.000000j | 0.001048+0.000000j | 0.001561-0.000000j | 0.002372-0.000000j | 0.003530-0.000000j | 0.005048-0.000000j | 0.006928+0.000000j | 0.009163+0.000000j | 0.011727-0.000000j | ... | 0.084583+0.000000j | 0.085252-0.000000j | 0.085848-0.000000j | 0.086372-0.000000j | 0.086827+0.000000j | 0.087214+0.000000j | 0.087535+0.000000j | 0.087790+0.000000j | 0.087983+0.000000j | 0.088113+0.000000j | |
| -2 | SG | PU | -0.000115-0.000000j | -0.000427-0.000000j | -0.000665+0.000000j | -0.000996-0.000000j | -0.001512-0.000000j | -0.002244-0.000000j | -0.003199-0.000000j | -0.004381-0.000000j | -0.005784-0.000000j | -0.007393-0.000000j | ... | -0.051392-0.000000j | -0.051726-0.000000j | -0.052010+0.000000j | -0.052248+0.000000j | -0.052440+0.000000j | -0.052587+0.000000j | -0.052690+0.000000j | -0.052750-0.000000j | -0.052766+0.000000j | -0.052741-0.000000j | |||
| 2 | SG | PU | -0.000115-0.000000j | -0.000427-0.000000j | -0.000665+0.000000j | -0.000996-0.000000j | -0.001512-0.000000j | -0.002244-0.000000j | -0.003199-0.000000j | -0.004381-0.000000j | -0.005784-0.000000j | -0.007393-0.000000j | ... | -0.051392-0.000000j | -0.051726-0.000000j | -0.052010+0.000000j | -0.052248+0.000000j | -0.052440+0.000000j | -0.052587+0.000000j | -0.052690+0.000000j | -0.052750-0.000000j | -0.052766+0.000000j | -0.052741-0.000000j | |||
| y | 0 | SG | PU | 0.000181-0.000000j | 0.000676+0.000000j | 0.001048+0.000000j | 0.001561-0.000000j | 0.002372-0.000000j | 0.003530-0.000000j | 0.005048-0.000000j | 0.006928-0.000000j | 0.009163-0.000000j | 0.011727-0.000000j | ... | 0.084583+0.000000j | 0.085252+0.000000j | 0.085848+0.000000j | 0.086372+0.000000j | 0.086827+0.000000j | 0.087214+0.000000j | 0.087535+0.000000j | 0.087790+0.000000j | 0.087983-0.000000j | 0.088113+0.000000j | ||
| -2 | SG | PU | 0.000115-0.000000j | 0.000427-0.000000j | 0.000665-0.000000j | 0.000996-0.000000j | 0.001512-0.000000j | 0.002244-0.000000j | 0.003199-0.000000j | 0.004381-0.000000j | 0.005784-0.000000j | 0.007393-0.000000j | ... | 0.051392-0.000000j | 0.051726-0.000000j | 0.052010-0.000000j | 0.052248-0.000000j | 0.052440-0.000000j | 0.052587-0.000000j | 0.052690+0.000000j | 0.052750-0.000000j | 0.052766-0.000000j | 0.052741-0.000000j | |||
| 2 | SG | PU | 0.000115-0.000000j | 0.000427+0.000000j | 0.000665-0.000000j | 0.000996+0.000000j | 0.001512+0.000000j | 0.002244+0.000000j | 0.003199+0.000000j | 0.004381-0.000000j | 0.005784+0.000000j | 0.007393+0.000000j | ... | 0.051392+0.000000j | 0.051726+0.000000j | 0.052010+0.000000j | 0.052248+0.000000j | 0.052440+0.000000j | 0.052587+0.000000j | 0.052690+0.000000j | 0.052750+0.000000j | 0.052766+0.000000j | 0.052741+0.000000j | |||
| 10 | x | 0 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.000134-0.000000j | ... | -0.008993-0.000000j | -0.009385+0.000000j | -0.009786+0.000000j | -0.010196+0.000000j | -0.010616+0.000000j | -0.011047+0.000000j | -0.011490-0.000000j | -0.011946+0.000000j | -0.012415-0.000000j | -0.012898-0.000000j | |
| -2 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.005321+0.000000j | 0.005549-0.000000j | 0.005782-0.000000j | 0.006019-0.000000j | 0.006262+0.000000j | 0.006512+0.000000j | 0.006767+0.000000j | 0.007030+0.000000j | 0.007299+0.000000j | 0.007577+0.000000j | |||
| 2 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.005321+0.000000j | 0.005549-0.000000j | 0.005782-0.000000j | 0.006019-0.000000j | 0.006262+0.000000j | 0.006512+0.000000j | 0.006767+0.000000j | 0.007030+0.000000j | 0.007299+0.000000j | 0.007577+0.000000j | |||
| y | 0 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.000134-0.000000j | ... | -0.008993+0.000000j | -0.009385+0.000000j | -0.009786-0.000000j | -0.010196+0.000000j | -0.010616+0.000000j | -0.011047-0.000000j | -0.011490+0.000000j | -0.011946+0.000000j | -0.012415+0.000000j | -0.012898+0.000000j | ||
| -2 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.005321+0.000000j | -0.005549+0.000000j | -0.005782+0.000000j | -0.006019+0.000000j | -0.006262+0.000000j | -0.006512+0.000000j | -0.006767+0.000000j | -0.007030+0.000000j | -0.007299+0.000000j | -0.007577+0.000000j | |||
| 2 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.005321-0.000000j | -0.005549-0.000000j | -0.005782-0.000000j | -0.006019-0.000000j | -0.006262-0.000000j | -0.006512-0.000000j | -0.006767-0.000000j | -0.007030-0.000000j | -0.007299-0.000000j | -0.007577-0.000000j | |||
| 12 | x | 0 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000625+0.000000j | 0.000674-0.000000j | 0.000726-0.000000j | 0.000781-0.000000j | 0.000839+0.000000j | 0.000901-0.000000j | 0.000967+0.000000j | 0.001037+0.000000j | 0.001111+0.000000j | 0.001190+0.000000j | |
| -2 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.000362+0.000000j | -0.000390+0.000000j | -0.000419+0.000000j | -0.000451+0.000000j | -0.000484+0.000000j | -0.000520+0.000000j | -0.000558-0.000000j | -0.000598-0.000000j | -0.000640-0.000000j | -0.000686-0.000000j | |||
| 2 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.000362+0.000000j | -0.000390+0.000000j | -0.000419+0.000000j | -0.000451+0.000000j | -0.000484+0.000000j | -0.000520+0.000000j | -0.000558-0.000000j | -0.000598-0.000000j | -0.000640-0.000000j | -0.000686-0.000000j | |||
| y | 0 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000625+0.000000j | 0.000674+0.000000j | 0.000726+0.000000j | 0.000781-0.000000j | 0.000839+0.000000j | 0.000901+0.000000j | 0.000967+0.000000j | 0.001037+0.000000j | 0.001111-0.000000j | 0.001190+0.000000j | ||
| -2 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000362-0.000000j | 0.000390-0.000000j | 0.000419-0.000000j | 0.000451-0.000000j | 0.000484-0.000000j | 0.000520+0.000000j | 0.000558-0.000000j | 0.000598-0.000000j | 0.000640-0.000000j | 0.000686-0.000000j | |||
| 2 | SG | PU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000362+0.000000j | 0.000390+0.000000j | 0.000419+0.000000j | 0.000451+0.000000j | 0.000484+0.000000j | 0.000520+0.000000j | 0.000558+0.000000j | 0.000598+0.000000j | 0.000640+0.000000j | 0.000686+0.000000j | |||
| SU | 0 | z | 0 | SG | SU | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | ... | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j |
| 2 | z | 0 | SG | SU | 0.784764-0.000000j | 0.292636+0.000000j | 0.110286-0.000000j | 0.047655+0.000000j | 0.053351-0.000000j | 0.100478-0.000000j | 0.172894-0.000000j | 0.260212-0.000000j | 0.355478-0.000000j | 0.453965-0.000000j | ... | 0.307136+0.000000j | 0.353015-0.000000j | 0.404836+0.000000j | 0.459405-0.000000j | 0.514462-0.000000j | 0.568485+0.000000j | 0.620505+0.000000j | 0.669947-0.000000j | 0.716512-0.000000j | 0.760083+0.000000j | |
| 4 | z | 0 | SG | SU | -0.040643+0.000000j | -0.472493-0.000000j | -0.596717-0.000000j | -0.603036-0.000000j | -0.543465+0.000000j | -0.445631+0.000000j | -0.326262-0.000000j | -0.196158-0.000000j | -0.062516+0.000000j | 0.069865-0.000000j | ... | -0.569503-0.000000j | -0.517657+0.000000j | -0.458173-0.000000j | -0.395217-0.000000j | -0.331713-0.000000j | -0.269614-0.000000j | -0.210149-0.000000j | -0.154034-0.000000j | -0.101629-0.000000j | -0.053060+0.000000j | |
| 6 | z | 0 | SG | SU | 0.067996+0.000000j | 0.124559+0.000000j | 0.181056-0.000000j | 0.236287+0.000000j | 0.289141-0.000000j | 0.338700-0.000000j | 0.384294-0.000000j | 0.425467-0.000000j | 0.461963-0.000000j | 0.493736-0.000000j | ... | -0.012438-0.000000j | -0.026005+0.000000j | -0.036082-0.000000j | -0.043618+0.000000j | -0.049363-0.000000j | -0.053889+0.000000j | -0.057618-0.000000j | -0.060854-0.000000j | -0.063810-0.000000j | -0.066634+0.000000j | |
| 8 | z | 0 | SG | SU | -0.000240-0.000000j | -0.000812-0.000000j | -0.001227-0.000000j | -0.001840-0.000000j | -0.002813+0.000000j | -0.004167-0.000000j | -0.005886+0.000000j | -0.007949-0.000000j | -0.010322-0.000000j | -0.012952-0.000000j | ... | 0.016562-0.000000j | 0.000498+0.000000j | -0.014200+0.000000j | -0.027442-0.000000j | -0.039244+0.000000j | -0.049687+0.000000j | -0.058880+0.000000j | -0.066945-0.000000j | -0.074001+0.000000j | -0.080160-0.000000j | |
| 10 | z | 0 | SG | SU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000137-0.000000j | ... | 0.036612+0.000000j | 0.039931+0.000000j | 0.042889+0.000000j | 0.045534-0.000000j | 0.047912+0.000000j | 0.050071+0.000000j | 0.052050+0.000000j | 0.053883+0.000000j | 0.055598+0.000000j | 0.057219+0.000000j | |
| 12 | z | 0 | SG | SU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.006051-0.000000j | -0.006437+0.000000j | -0.006788-0.000000j | -0.007113+0.000000j | -0.007416+0.000000j | -0.007706-0.000000j | -0.007985+0.000000j | -0.008259+0.000000j | -0.008530+0.000000j | -0.008801-0.000000j | |
| 14 | z | 0 | SG | SU | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000422+0.000000j | 0.000449+0.000000j | 0.000476+0.000000j | 0.000501+0.000000j | 0.000525+0.000000j | 0.000549+0.000000j | 0.000573+0.000000j | 0.000598+0.000000j | 0.000622+0.000000j | 0.000648+0.000000j |
46 rows × 51 columns
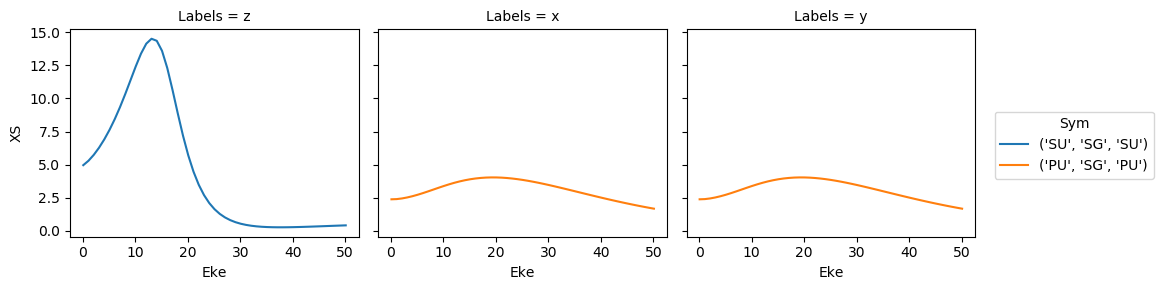
Here all the \(\beta_{LM}\) are normalised, hence the X-sections are unity. For the \(N_2\) case (linear, :math:`D_{infty h} symmetry <https://en.wikipedia.org/wiki/Molecular_symmetry>`__), note the correlation of symmetry groups with polarization geometries (SU > z; PU > x,y).
As a further test, we can check abs terms x pol == y pol - there should only be a rotation (phase) difference between the results for these polarization geometries
[7]:
testSub = mTermST.sel({'Labels':'x'}).pipe(np.abs) - mTermST.sel({'Labels':'y'}).pipe(np.abs)
print(f"Min difference: {testSub.min().data}, max difference: {testSub.max().data}")
Min difference: -3.3306690738754696e-16, max difference: 3.3306690738754696e-16
The X-sections are stored sepearately in the output Xarray:
[8]:
mTermST.XS.real.squeeze().plot.line(x='Eke', col='Labels');
C:\Program Files (x86)\Microsoft Visual Studio\Shared\Anaconda3_64\envs\ePSdev\lib\site-packages\xarray\plot\plot.py:86: FutureWarning:
This DataArray contains multi-dimensional coordinates. In the future, these coordinates will be transposed as well unless you specify transpose_coords=False.
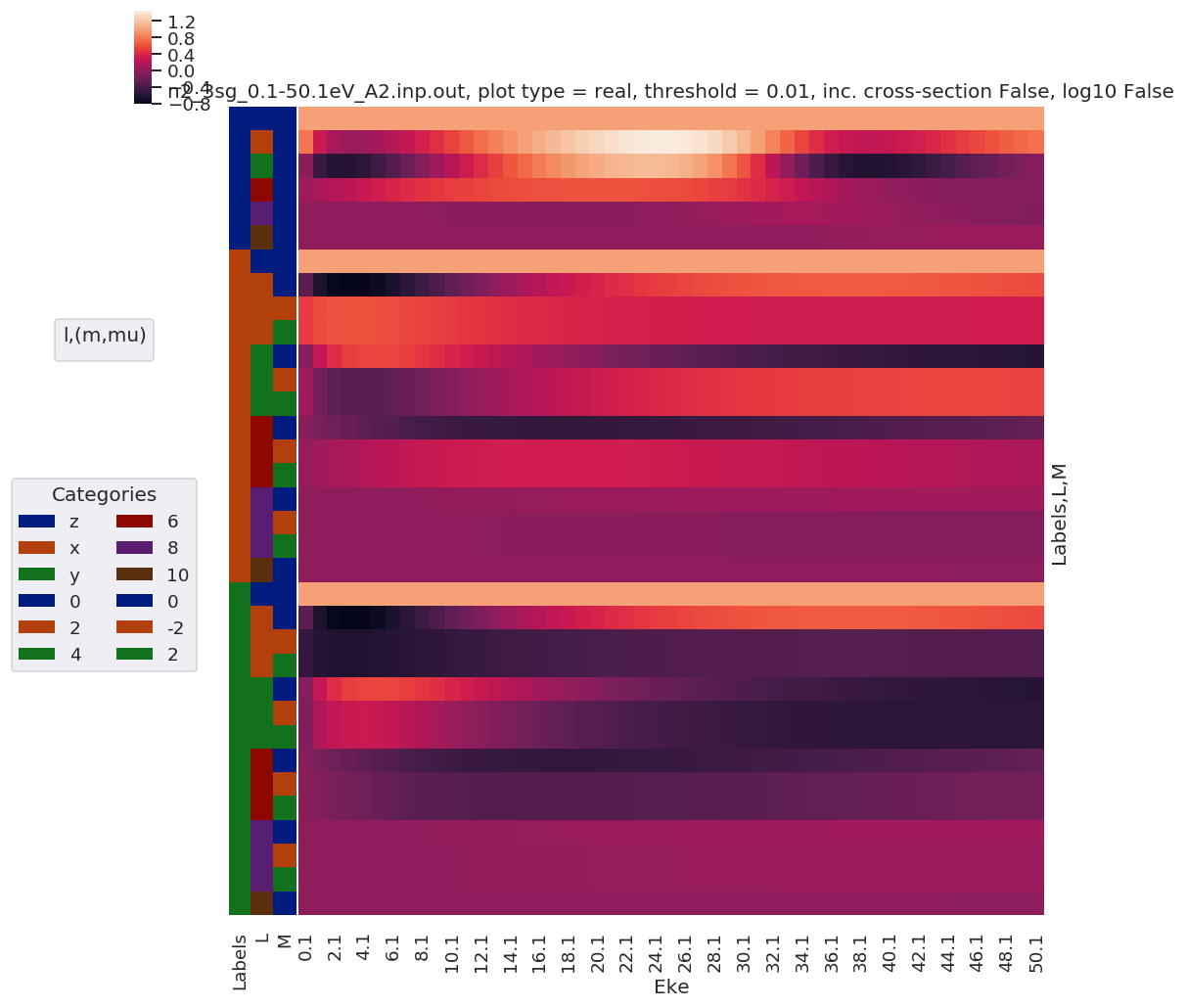
With symmetry summation
This produces simpler results, summed over continua.
[9]:
symSum = True # Sum over symmetry groups, or keep separate?
start = time.time()
mTermST, mTermS, mTermTest = ep.geomFunc.mfblmXprod(dataSet[0], QNs = None, thres = thres, selDims = {'it':1, 'Type':'L'}, thresDims='Eke', RX=RX, symSum=symSum, SFflag=True, phaseConvention=phaseConvention)
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points, {2} polarizations, threshold={3}.'.format((end-start), mTermST.Eke.size, RX.size, thres))
# Elapsed time = 1.704383134841919 seconds, for 51 energy points, 3 polarizations, threshold=threshold=0.01.
# Elapsed time = 3.151679754257202 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
Elapsed time = 3.079366445541382 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
[10]:
# Full results (before summation)
mTermST.attrs['dataType'] = 'matE' # Set matE here to allow for correct plotting of sym dims.
plotDimsRed = ['Labels','L','M'] # Set plotDims to fix dim ordering in plot
if not symSum:
plotDimsRed.extend(['Cont','Targ','Total'])
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, plotDims=plotDimsRed, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True, SFflag=False)
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True) # If plotDims is not passed use default ordering.
Plotting data n2_3sg_0.1-50.1eV_A2.inp.out, pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[11]:
# Tabulate complex values...
mTermSTpd, _ = ep.util.multiDimXrToPD(mTermST, colDims='Eke', thres = thres)
mTermSTpd
[11]:
| Eke | 0.1 | 1.1 | 2.1 | 3.1 | 4.1 | 5.1 | 6.1 | 7.1 | 8.1 | 9.1 | ... | 41.1 | 42.1 | 43.1 | 44.1 | 45.1 | 46.1 | 47.1 | 48.1 | 49.1 | 50.1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | Labels | M | |||||||||||||||||||||
| 0 | z | 0 | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | ... | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j |
| x | 0 | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | ... | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | |
| y | 0 | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | 1.000000-0.000000j | ... | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | 1.000000+0.000000j | |
| 2 | z | 0 | 0.784764-0.000000j | 0.292636+0.000000j | 0.110286-0.000000j | 0.047655+0.000000j | 0.053351-0.000000j | 0.100478-0.000000j | 0.172894-0.000000j | 0.260212-0.000000j | 0.355478-0.000000j | 0.453965-0.000000j | ... | 0.307136+0.000000j | 0.353015-0.000000j | 0.404836+0.000000j | 0.459405-0.000000j | 0.514462-0.000000j | 0.568485+0.000000j | 0.620505+0.000000j | 0.669947-0.000000j | 0.716512-0.000000j | 0.760083+0.000000j |
| x | 0 | -0.272711-0.000000j | -0.638474-0.000000j | -0.775003-0.000000j | -0.814436-0.000000j | -0.794373+0.000000j | -0.736632+0.000000j | -0.655845-0.000000j | -0.562321-0.000000j | -0.463340-0.000000j | -0.363902-0.000000j | ... | 0.655141+0.000000j | 0.650741+0.000000j | 0.645402-0.000000j | 0.639166-0.000000j | 0.632075-0.000000j | 0.624163+0.000000j | 0.615465+0.000000j | 0.606012+0.000000j | 0.595832+0.000000j | 0.584952+0.000000j | |
| -2 | 0.512102-0.000000j | 0.586763+0.000000j | 0.614632-0.000000j | 0.622681-0.000000j | 0.618586-0.000000j | 0.606800-0.000000j | 0.590309-0.000000j | 0.571219+0.000000j | 0.551014+0.000000j | 0.530717-0.000000j | ... | 0.322705+0.000000j | 0.323603+0.000000j | 0.324693-0.000000j | 0.325966-0.000000j | 0.327414+0.000000j | 0.329029+0.000000j | 0.330804+0.000000j | 0.332734+0.000000j | 0.334812+0.000000j | 0.337033+0.000000j | ||
| 2 | 0.512102-0.000000j | 0.586763+0.000000j | 0.614632-0.000000j | 0.622681-0.000000j | 0.618586-0.000000j | 0.606800-0.000000j | 0.590309-0.000000j | 0.571219+0.000000j | 0.551014+0.000000j | 0.530717-0.000000j | ... | 0.322705+0.000000j | 0.323603+0.000000j | 0.324693-0.000000j | 0.325966-0.000000j | 0.327414+0.000000j | 0.329029+0.000000j | 0.330804+0.000000j | 0.332734+0.000000j | 0.334812+0.000000j | 0.337033+0.000000j | ||
| y | 0 | -0.272711+0.000000j | -0.638474-0.000000j | -0.775003-0.000000j | -0.814436-0.000000j | -0.794373+0.000000j | -0.736632-0.000000j | -0.655845-0.000000j | -0.562321-0.000000j | -0.463340-0.000000j | -0.363902-0.000000j | ... | 0.655141+0.000000j | 0.650741-0.000000j | 0.645402+0.000000j | 0.639166+0.000000j | 0.632075+0.000000j | 0.624163+0.000000j | 0.615465+0.000000j | 0.606012-0.000000j | 0.595832-0.000000j | 0.584952+0.000000j | |
| -2 | -0.512102+0.000000j | -0.586763+0.000000j | -0.614632+0.000000j | -0.622681+0.000000j | -0.618586+0.000000j | -0.606800+0.000000j | -0.590309+0.000000j | -0.571219+0.000000j | -0.551014+0.000000j | -0.530717+0.000000j | ... | -0.322705+0.000000j | -0.323603+0.000000j | -0.324693+0.000000j | -0.325966+0.000000j | -0.327414+0.000000j | -0.329029+0.000000j | -0.330804+0.000000j | -0.332734+0.000000j | -0.334812+0.000000j | -0.337033+0.000000j | ||
| 2 | -0.512102-0.000000j | -0.586763-0.000000j | -0.614632-0.000000j | -0.622681-0.000000j | -0.618586-0.000000j | -0.606800-0.000000j | -0.590309-0.000000j | -0.571219-0.000000j | -0.551014-0.000000j | -0.530717-0.000000j | ... | -0.322705-0.000000j | -0.323603-0.000000j | -0.324693-0.000000j | -0.325966-0.000000j | -0.327414-0.000000j | -0.329029-0.000000j | -0.330804-0.000000j | -0.332734-0.000000j | -0.334812-0.000000j | -0.337033-0.000000j | ||
| 4 | z | 0 | -0.040643+0.000000j | -0.472493-0.000000j | -0.596717-0.000000j | -0.603036-0.000000j | -0.543465+0.000000j | -0.445631+0.000000j | -0.326262-0.000000j | -0.196158-0.000000j | -0.062516+0.000000j | 0.069865-0.000000j | ... | -0.569503-0.000000j | -0.517657+0.000000j | -0.458173-0.000000j | -0.395217-0.000000j | -0.331713-0.000000j | -0.269614-0.000000j | -0.210149-0.000000j | -0.154034-0.000000j | -0.101629-0.000000j | -0.053060+0.000000j |
| x | 0 | -0.059474-0.000000j | 0.271217+0.000000j | 0.432955-0.000000j | 0.521218-0.000000j | 0.562256-0.000000j | 0.570921-0.000000j | 0.557098-0.000000j | 0.527855+0.000000j | 0.488402+0.000000j | 0.442583-0.000000j | ... | -0.522724+0.000000j | -0.532915+0.000000j | -0.542405+0.000000j | -0.551224+0.000000j | -0.559398+0.000000j | -0.566951-0.000000j | -0.573903-0.000000j | -0.580274-0.000000j | -0.586083+0.000000j | -0.591343+0.000000j | |
| -2 | 0.080503-0.000000j | -0.153387-0.000000j | -0.252803-0.000000j | -0.294656-0.000000j | -0.300540-0.000000j | -0.282866+0.000000j | -0.249932-0.000000j | -0.207619-0.000000j | -0.160148-0.000000j | -0.110502-0.000000j | ... | 0.555041+0.000000j | 0.556708+0.000000j | 0.557821-0.000000j | 0.558406+0.000000j | 0.558483+0.000000j | 0.558074+0.000000j | 0.557198-0.000000j | 0.555870+0.000000j | 0.554108+0.000000j | 0.551925+0.000000j | ||
| 2 | 0.080503-0.000000j | -0.153387-0.000000j | -0.252803-0.000000j | -0.294656-0.000000j | -0.300540-0.000000j | -0.282866+0.000000j | -0.249932-0.000000j | -0.207619-0.000000j | -0.160148-0.000000j | -0.110502-0.000000j | ... | 0.555041+0.000000j | 0.556708+0.000000j | 0.557821-0.000000j | 0.558406+0.000000j | 0.558483+0.000000j | 0.558074+0.000000j | 0.557198-0.000000j | 0.555870+0.000000j | 0.554108+0.000000j | 0.551925+0.000000j | ||
| y | 0 | -0.059474-0.000000j | 0.271217+0.000000j | 0.432955+0.000000j | 0.521218-0.000000j | 0.562256-0.000000j | 0.570921-0.000000j | 0.557098+0.000000j | 0.527855-0.000000j | 0.488402-0.000000j | 0.442583-0.000000j | ... | -0.522724+0.000000j | -0.532915+0.000000j | -0.542405-0.000000j | -0.551224+0.000000j | -0.559398+0.000000j | -0.566951-0.000000j | -0.573903-0.000000j | -0.580274-0.000000j | -0.586083+0.000000j | -0.591343+0.000000j | |
| -2 | -0.080503+0.000000j | 0.153387-0.000000j | 0.252803-0.000000j | 0.294656-0.000000j | 0.300540-0.000000j | 0.282866-0.000000j | 0.249932-0.000000j | 0.207619-0.000000j | 0.160148-0.000000j | 0.110502-0.000000j | ... | -0.555041+0.000000j | -0.556708+0.000000j | -0.557821+0.000000j | -0.558406+0.000000j | -0.558483+0.000000j | -0.558074+0.000000j | -0.557198+0.000000j | -0.555870+0.000000j | -0.554108+0.000000j | -0.551925+0.000000j | ||
| 2 | -0.080503+0.000000j | 0.153387+0.000000j | 0.252803+0.000000j | 0.294656+0.000000j | 0.300540+0.000000j | 0.282866+0.000000j | 0.249932+0.000000j | 0.207619+0.000000j | 0.160148+0.000000j | 0.110502+0.000000j | ... | -0.555041-0.000000j | -0.556708-0.000000j | -0.557821-0.000000j | -0.558406-0.000000j | -0.558483-0.000000j | -0.558074-0.000000j | -0.557198-0.000000j | -0.555870-0.000000j | -0.554108-0.000000j | -0.551925-0.000000j | ||
| 6 | z | 0 | 0.067996+0.000000j | 0.124559+0.000000j | 0.181056-0.000000j | 0.236287+0.000000j | 0.289141-0.000000j | 0.338700-0.000000j | 0.384294-0.000000j | 0.425467-0.000000j | 0.461963-0.000000j | 0.493736-0.000000j | ... | -0.012438-0.000000j | -0.026005+0.000000j | -0.036082-0.000000j | -0.043618+0.000000j | -0.049363-0.000000j | -0.053889+0.000000j | -0.057618-0.000000j | -0.060854-0.000000j | -0.063810-0.000000j | -0.066634+0.000000j |
| x | 0 | -0.058944+0.000000j | -0.107815-0.000000j | -0.158159+0.000000j | -0.207754-0.000000j | -0.255279-0.000000j | -0.299612+0.000000j | -0.339916-0.000000j | -0.375688-0.000000j | -0.406740-0.000000j | -0.433136-0.000000j | ... | -0.334833+0.000000j | -0.323955+0.000000j | -0.312985+0.000000j | -0.301929+0.000000j | -0.290790+0.000000j | -0.279573+0.000000j | -0.268281+0.000000j | -0.256919+0.000000j | -0.245491-0.000000j | -0.234000+0.000000j | |
| -2 | 0.040201-0.000000j | 0.073410+0.000000j | 0.107661+0.000000j | 0.141347-0.000000j | 0.173516-0.000000j | 0.203384-0.000000j | 0.230377-0.000000j | 0.254147+0.000000j | 0.274568+0.000000j | 0.291696-0.000000j | ... | 0.201422+0.000000j | 0.193886+0.000000j | 0.186317-0.000000j | 0.178717-0.000000j | 0.171088+0.000000j | 0.163434+0.000000j | 0.155756+0.000000j | 0.148057+0.000000j | 0.140340-0.000000j | 0.132606+0.000000j | ||
| 2 | 0.040201-0.000000j | 0.073410+0.000000j | 0.107661+0.000000j | 0.141347-0.000000j | 0.173516-0.000000j | 0.203384-0.000000j | 0.230377-0.000000j | 0.254147+0.000000j | 0.274568+0.000000j | 0.291696-0.000000j | ... | 0.201422+0.000000j | 0.193886+0.000000j | 0.186317-0.000000j | 0.178717+0.000000j | 0.171088+0.000000j | 0.163434+0.000000j | 0.155756+0.000000j | 0.148057+0.000000j | 0.140340-0.000000j | 0.132606+0.000000j | ||
| y | 0 | -0.058944+0.000000j | -0.107815-0.000000j | -0.158159-0.000000j | -0.207754+0.000000j | -0.255279-0.000000j | -0.299612+0.000000j | -0.339916+0.000000j | -0.375688-0.000000j | -0.406740-0.000000j | -0.433136-0.000000j | ... | -0.334833+0.000000j | -0.323955+0.000000j | -0.312985+0.000000j | -0.301929+0.000000j | -0.290790+0.000000j | -0.279573-0.000000j | -0.268281-0.000000j | -0.256919+0.000000j | -0.245491+0.000000j | -0.234000+0.000000j | |
| -2 | -0.040201+0.000000j | -0.073410+0.000000j | -0.107661+0.000000j | -0.141347+0.000000j | -0.173516+0.000000j | -0.203384+0.000000j | -0.230377-0.000000j | -0.254147+0.000000j | -0.274568+0.000000j | -0.291696+0.000000j | ... | -0.201422+0.000000j | -0.193886+0.000000j | -0.186317+0.000000j | -0.178717+0.000000j | -0.171088+0.000000j | -0.163434+0.000000j | -0.155756+0.000000j | -0.148057+0.000000j | -0.140340+0.000000j | -0.132606+0.000000j | ||
| 2 | -0.040201-0.000000j | -0.073410-0.000000j | -0.107661-0.000000j | -0.141347-0.000000j | -0.173516-0.000000j | -0.203384-0.000000j | -0.230377-0.000000j | -0.254147-0.000000j | -0.274568-0.000000j | -0.291696-0.000000j | ... | -0.201422-0.000000j | -0.193886-0.000000j | -0.186317-0.000000j | -0.178717-0.000000j | -0.171088-0.000000j | -0.163434-0.000000j | -0.155756-0.000000j | -0.148057-0.000000j | -0.140340-0.000000j | -0.132606-0.000000j | ||
| 8 | z | 0 | -0.000240-0.000000j | -0.000812-0.000000j | -0.001227-0.000000j | -0.001840-0.000000j | -0.002813+0.000000j | -0.004167-0.000000j | -0.005886+0.000000j | -0.007949-0.000000j | -0.010322-0.000000j | -0.012952-0.000000j | ... | 0.016562-0.000000j | 0.000498+0.000000j | -0.014200+0.000000j | -0.027442-0.000000j | -0.039244+0.000000j | -0.049687+0.000000j | -0.058880+0.000000j | -0.066945-0.000000j | -0.074001+0.000000j | -0.080160-0.000000j |
| x | 0 | 0.000181-0.000000j | 0.000676+0.000000j | 0.001048+0.000000j | 0.001561-0.000000j | 0.002372-0.000000j | 0.003530-0.000000j | 0.005048-0.000000j | 0.006928+0.000000j | 0.009163+0.000000j | 0.011727-0.000000j | ... | 0.084583+0.000000j | 0.085252-0.000000j | 0.085848-0.000000j | 0.086372-0.000000j | 0.086827+0.000000j | 0.087214+0.000000j | 0.087535+0.000000j | 0.087790+0.000000j | 0.087983+0.000000j | 0.088113+0.000000j | |
| -2 | -0.000115-0.000000j | -0.000427-0.000000j | -0.000665+0.000000j | -0.000996-0.000000j | -0.001512-0.000000j | -0.002244-0.000000j | -0.003199-0.000000j | -0.004381-0.000000j | -0.005784-0.000000j | -0.007393-0.000000j | ... | -0.051392-0.000000j | -0.051726-0.000000j | -0.052010+0.000000j | -0.052248+0.000000j | -0.052440+0.000000j | -0.052587+0.000000j | -0.052690+0.000000j | -0.052750-0.000000j | -0.052766+0.000000j | -0.052741-0.000000j | ||
| 2 | -0.000115-0.000000j | -0.000427-0.000000j | -0.000665+0.000000j | -0.000996-0.000000j | -0.001512-0.000000j | -0.002244-0.000000j | -0.003199-0.000000j | -0.004381-0.000000j | -0.005784-0.000000j | -0.007393-0.000000j | ... | -0.051392-0.000000j | -0.051726-0.000000j | -0.052010+0.000000j | -0.052248+0.000000j | -0.052440+0.000000j | -0.052587+0.000000j | -0.052690+0.000000j | -0.052750-0.000000j | -0.052766+0.000000j | -0.052741-0.000000j | ||
| y | 0 | 0.000181-0.000000j | 0.000676+0.000000j | 0.001048+0.000000j | 0.001561-0.000000j | 0.002372-0.000000j | 0.003530-0.000000j | 0.005048-0.000000j | 0.006928-0.000000j | 0.009163-0.000000j | 0.011727-0.000000j | ... | 0.084583+0.000000j | 0.085252+0.000000j | 0.085848+0.000000j | 0.086372+0.000000j | 0.086827+0.000000j | 0.087214+0.000000j | 0.087535+0.000000j | 0.087790+0.000000j | 0.087983-0.000000j | 0.088113+0.000000j | |
| -2 | 0.000115-0.000000j | 0.000427-0.000000j | 0.000665-0.000000j | 0.000996-0.000000j | 0.001512-0.000000j | 0.002244-0.000000j | 0.003199-0.000000j | 0.004381-0.000000j | 0.005784-0.000000j | 0.007393-0.000000j | ... | 0.051392-0.000000j | 0.051726-0.000000j | 0.052010-0.000000j | 0.052248-0.000000j | 0.052440-0.000000j | 0.052587-0.000000j | 0.052690+0.000000j | 0.052750-0.000000j | 0.052766-0.000000j | 0.052741-0.000000j | ||
| 2 | 0.000115-0.000000j | 0.000427+0.000000j | 0.000665-0.000000j | 0.000996+0.000000j | 0.001512+0.000000j | 0.002244+0.000000j | 0.003199+0.000000j | 0.004381-0.000000j | 0.005784+0.000000j | 0.007393+0.000000j | ... | 0.051392+0.000000j | 0.051726+0.000000j | 0.052010+0.000000j | 0.052248+0.000000j | 0.052440+0.000000j | 0.052587+0.000000j | 0.052690+0.000000j | 0.052750+0.000000j | 0.052766+0.000000j | 0.052741+0.000000j | ||
| 10 | z | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000137-0.000000j | ... | 0.036612+0.000000j | 0.039931+0.000000j | 0.042889+0.000000j | 0.045534-0.000000j | 0.047912+0.000000j | 0.050071+0.000000j | 0.052050+0.000000j | 0.053883+0.000000j | 0.055598+0.000000j | 0.057219+0.000000j |
| x | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.000134-0.000000j | ... | -0.008993-0.000000j | -0.009385+0.000000j | -0.009786+0.000000j | -0.010196+0.000000j | -0.010616+0.000000j | -0.011047+0.000000j | -0.011490-0.000000j | -0.011946+0.000000j | -0.012415-0.000000j | -0.012898-0.000000j | |
| -2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.005321+0.000000j | 0.005549-0.000000j | 0.005782-0.000000j | 0.006019-0.000000j | 0.006262+0.000000j | 0.006512+0.000000j | 0.006767+0.000000j | 0.007030+0.000000j | 0.007299+0.000000j | 0.007577+0.000000j | ||
| 2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.005321+0.000000j | 0.005549-0.000000j | 0.005782-0.000000j | 0.006019-0.000000j | 0.006262+0.000000j | 0.006512+0.000000j | 0.006767+0.000000j | 0.007030+0.000000j | 0.007299+0.000000j | 0.007577+0.000000j | ||
| y | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.000134-0.000000j | ... | -0.008993+0.000000j | -0.009385+0.000000j | -0.009786-0.000000j | -0.010196+0.000000j | -0.010616+0.000000j | -0.011047-0.000000j | -0.011490+0.000000j | -0.011946+0.000000j | -0.012415+0.000000j | -0.012898+0.000000j | |
| -2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.005321+0.000000j | -0.005549+0.000000j | -0.005782+0.000000j | -0.006019+0.000000j | -0.006262+0.000000j | -0.006512+0.000000j | -0.006767+0.000000j | -0.007030+0.000000j | -0.007299+0.000000j | -0.007577+0.000000j | ||
| 2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.005321-0.000000j | -0.005549-0.000000j | -0.005782-0.000000j | -0.006019-0.000000j | -0.006262-0.000000j | -0.006512-0.000000j | -0.006767-0.000000j | -0.007030-0.000000j | -0.007299-0.000000j | -0.007577-0.000000j | ||
| 12 | z | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.006051-0.000000j | -0.006437+0.000000j | -0.006788-0.000000j | -0.007113+0.000000j | -0.007416+0.000000j | -0.007706-0.000000j | -0.007985+0.000000j | -0.008259+0.000000j | -0.008530+0.000000j | -0.008801-0.000000j |
| x | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000625+0.000000j | 0.000674-0.000000j | 0.000726-0.000000j | 0.000781-0.000000j | 0.000839+0.000000j | 0.000901-0.000000j | 0.000967+0.000000j | 0.001037+0.000000j | 0.001111+0.000000j | 0.001190+0.000000j | |
| -2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.000362+0.000000j | -0.000390+0.000000j | -0.000419+0.000000j | -0.000451+0.000000j | -0.000484+0.000000j | -0.000520+0.000000j | -0.000558-0.000000j | -0.000598-0.000000j | -0.000640-0.000000j | -0.000686-0.000000j | ||
| 2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | -0.000362+0.000000j | -0.000390+0.000000j | -0.000419+0.000000j | -0.000451+0.000000j | -0.000484+0.000000j | -0.000520+0.000000j | -0.000558-0.000000j | -0.000598-0.000000j | -0.000640-0.000000j | -0.000686-0.000000j | ||
| y | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000625+0.000000j | 0.000674+0.000000j | 0.000726+0.000000j | 0.000781-0.000000j | 0.000839+0.000000j | 0.000901+0.000000j | 0.000967+0.000000j | 0.001037+0.000000j | 0.001111-0.000000j | 0.001190+0.000000j | |
| -2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000362-0.000000j | 0.000390-0.000000j | 0.000419-0.000000j | 0.000451-0.000000j | 0.000484-0.000000j | 0.000520+0.000000j | 0.000558-0.000000j | 0.000598-0.000000j | 0.000640-0.000000j | 0.000686-0.000000j | ||
| 2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000362+0.000000j | 0.000390+0.000000j | 0.000419+0.000000j | 0.000451+0.000000j | 0.000484+0.000000j | 0.000520+0.000000j | 0.000558+0.000000j | 0.000598+0.000000j | 0.000640+0.000000j | 0.000686+0.000000j | ||
| 14 | z | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | 0.000422+0.000000j | 0.000449+0.000000j | 0.000476+0.000000j | 0.000501+0.000000j | 0.000525+0.000000j | 0.000549+0.000000j | 0.000573+0.000000j | 0.000598+0.000000j | 0.000622+0.000000j | 0.000648+0.000000j |
46 rows × 51 columns
[12]:
mTermST.XS.real.squeeze().plot.line(x='Eke', col='Labels');
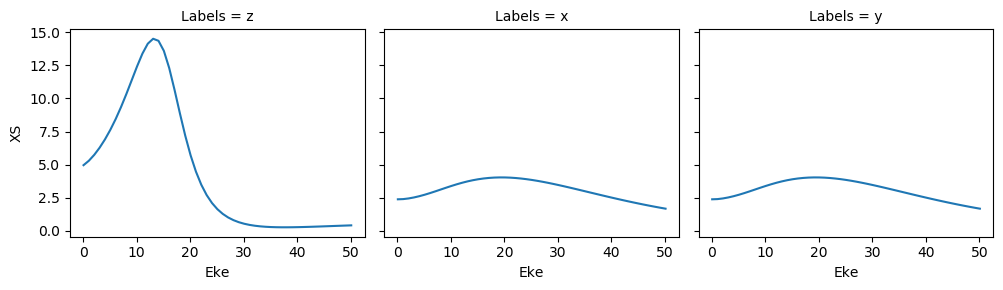
Verification - test vs. existing calcs
The existing method, implemented in mfblm(), makes use of a set of nested loops; this is far from optimal and rather slow (although could be sped up with parallel methods).
N2
[13]:
daIn = dataSet[0].copy()
# BLMXeN2 = ep.mfblm(daIn[:, 1:4], selDims = {'Type':'L'}, thres = 1e-4) # Subselected on Eke
start = time.time()
BLMXeN2 = ep.mfblm(daIn, selDims = selDims, thres = thres, verbose = False) # Run for all Eke. Note this fails if selDims = None, to fix!
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points, single pol geom, thres={2}.'.format((end-start), BLMXeN2.Eke.size, thres))
Elapsed time = 24.903498649597168 seconds, for 51 energy points, single pol geom, thres=0.0001.
[14]:
# Set standard pol geoms (== (z,x,y) as used above)
eAngs = ep.setPolGeoms()
# Calculate for each pol geom
start = time.time()
BLM = ep.mfblmEuler(dataSet[0], selDims=selDims, eAngs = eAngs, thres = thres, SFflag = True, verbose = 0) # Run for all Eke. Note this fails if selDims = None, to fix!
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points, {2} polarisations, threshold={3}.'.format((end-start), BLM.Eke.size, eAngs.size, thres))
# Elapsed time = 35.40217471122742 seconds, for 51 energy points, 3 polarisations, threshold=0.01.
# Elapsed time = 77.12336850166321 seconds, for 51 energy points, 3 polarisations, threshold=0.0001.
Elapsed time = 74.48245048522949 seconds, for 51 energy points, 3 polarisations, threshold=0.0001.
[15]:
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(BLM.swap_dims({'Euler':'Labels'}), SFflag = False, eulerGroup = True, fillna = True)
Plotting data n2_3sg_0.1-50.1eV_A2.inp.out, pType=a, thres=0.01, with Seaborn
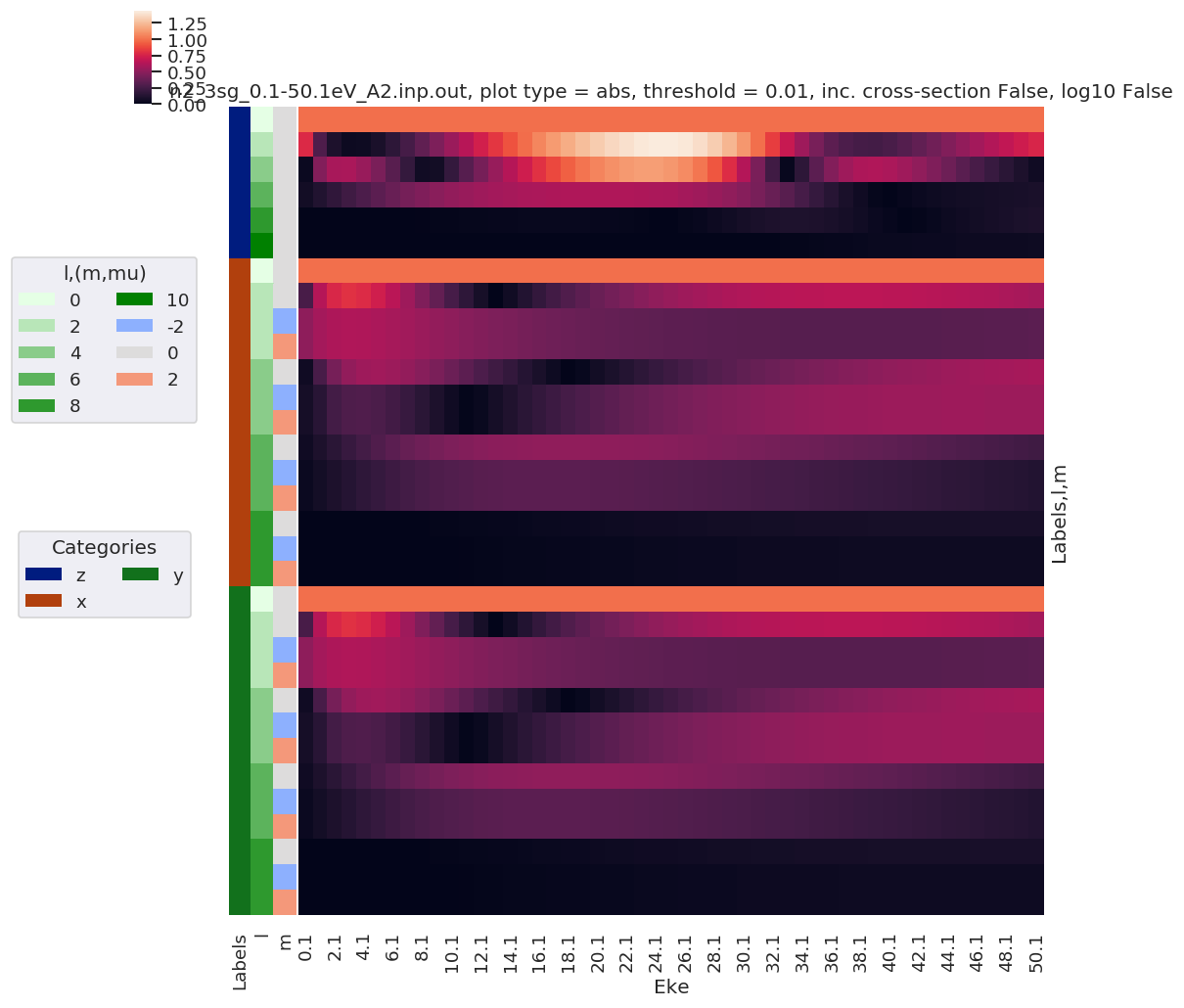
[16]:
BLMrename = BLM.swap_dims({'Euler':'Labels'}).unstack('BLM').rename({'l':'L','m':'M'}).stack({'LM':['L','M']}) # Reformat Xarray
testSub = mTermST - BLMrename
testSub.attrs['dataType']='matE'
[17]:
print(f"Min difference: {testSub.min().data}, max difference: {testSub.max().data}, threshold: {thres}")
# For thres = 1e-4, max diff = 0.0289
# For thres = 1e-2, max diff = 0.3781
Min difference: (-0.01001260432521213-1.9073640679125083e-17j), max difference: (0.02883058068349678+1.7578510363291103e-17j), threshold: 0.0001
TODO: Difference is >theshold here, so need to check differences in more detail. Due to difference in thresholding and accumulation in fns?
[18]:
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testSub, xDim='Eke', SFflag = False, fillna = True, thres = None)
Plotting data (No filename), pType=a, thres=None, with Seaborn
No handles with labels found to put in legend.
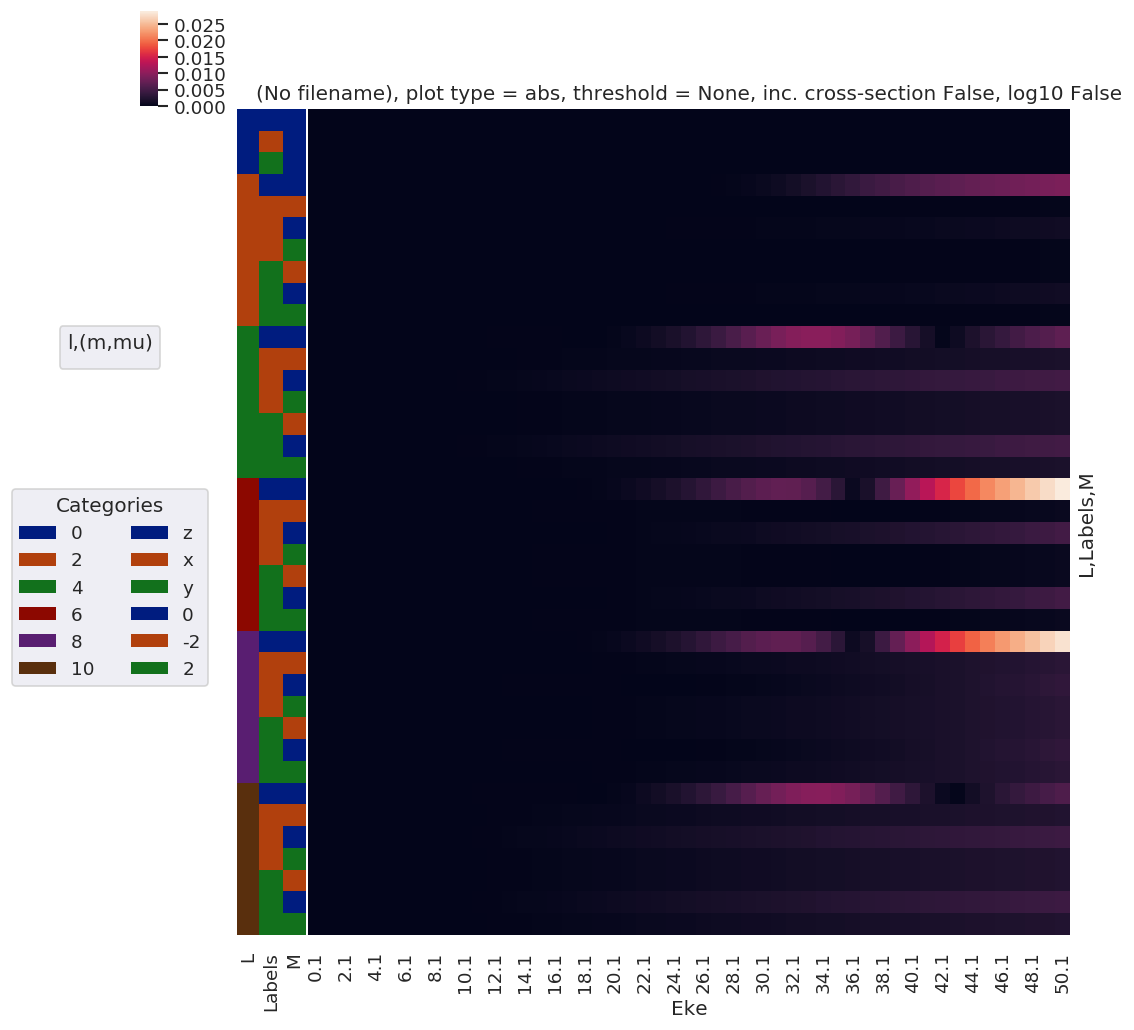
[19]:
# Check pol geoms as before
testSubXY = mTermST.sel({'Labels':'x'}).pipe(np.abs) - mTermST.sel({'Labels':'y'}).pipe(np.abs)
print(f"Min difference: {testSubXY.min().data}, max difference: {testSubXY.max().data}")
Min difference: -3.3306690738754696e-16, max difference: 3.3306690738754696e-16
[20]:
# Normalize and plot results - Original mfblm() results vs. geomFunc case
BLM.XS.real.squeeze().plot.line(x='Eke', col='Euler');
# mTermST.XS.sum(['Cont', 'Total']).real.squeeze().plot.line(x='Eke', col='Labels');
mTermST.XS.real.squeeze().plot.line(x='Eke', col='Labels');
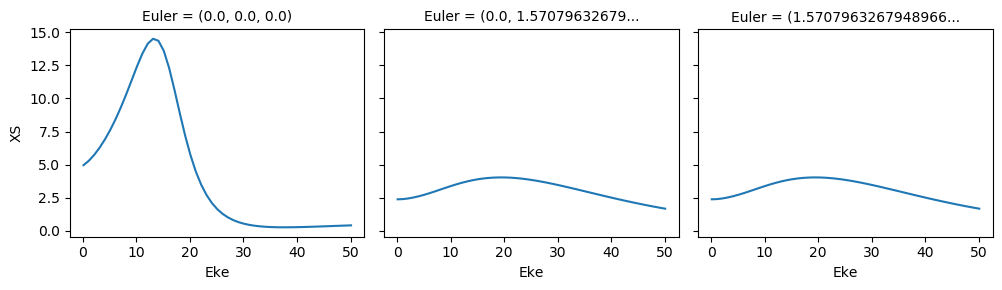
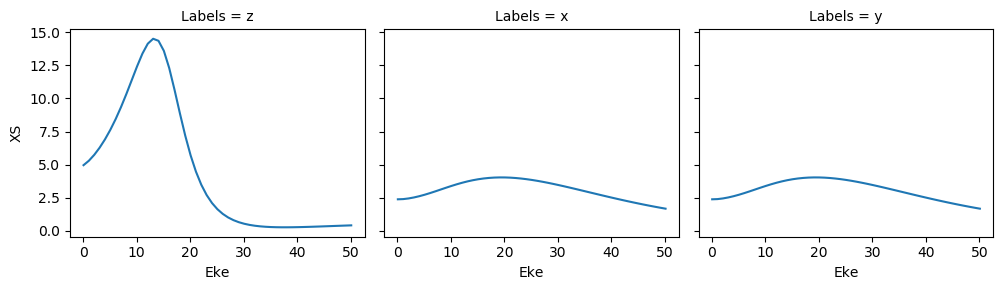
[21]:
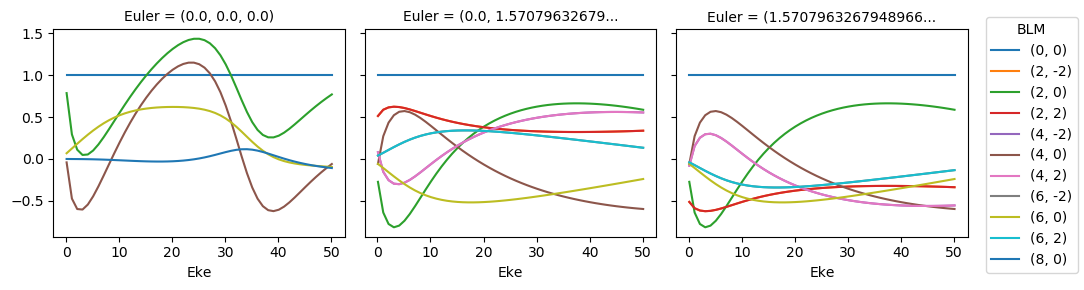
# Normalize and plot results - BLM values vs. polarisation geometry
ep.util.matEleSelector(BLM, thres = 0.1, dims='Eke').real.squeeze().plot.line(x='Eke', col='Euler');
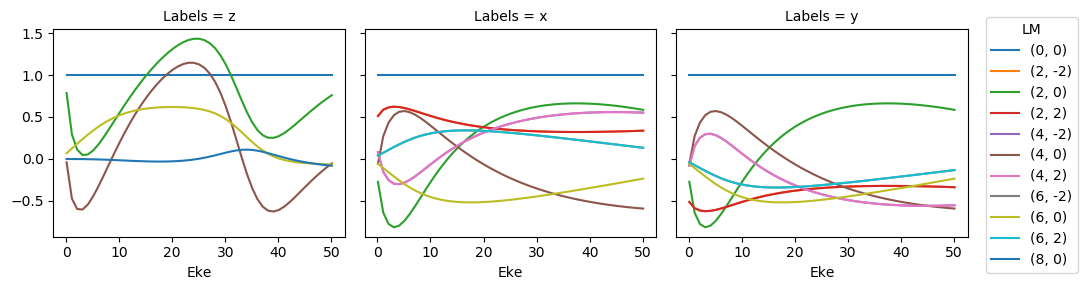
ep.util.matEleSelector(mTermST, thres = 0.1, dims='Eke').real.squeeze().plot.line(x='Eke', col='Labels');
# Replot differences as before - looks like E-dependence, so likely handling of SF (scale factor) is the issue here.
ep.util.matEleSelector(testSub, thres = 1e-4, dims='Eke').real.squeeze().plot.line(x='Eke', col='Labels');
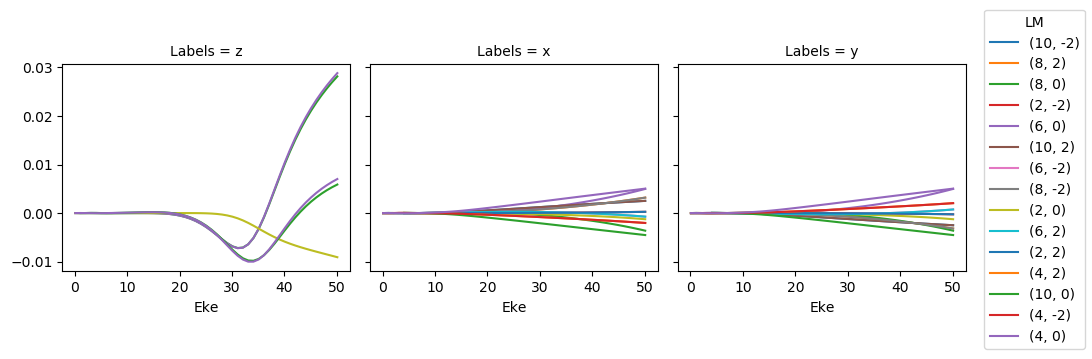
NO2
Non-linear, 3 symmetry groups.
[22]:
# Load data from modPath\data
dataPath = os.path.join(modPath, 'data', 'photoionization')
dataFile = os.path.join(dataPath, 'no2_demo_ePS.out') # Set for sample N2 data for testing
# Scan data file
dataSet = ep.readMatEle(fileIn = dataFile)
dataXS = ep.readMatEle(fileIn = dataFile, recordType = 'CrossSection') # XS info currently not set in NO2 sample file.
*** ePSproc readMatEle(): scanning files for DumpIdy segments.
*** Scanning file(s)
['D:\\code\\github\\ePSproc\\data\\photoionization\\no2_demo_ePS.out']
*** Reading ePS output file: D:\code\github\ePSproc\data\photoionization\no2_demo_ePS.out
Expecting 1 energy points.
Expecting 3 symmetries.
Scanning CrossSection segments.
Expecting 3 DumpIdy segments.
Found 3 dumpIdy segments (sets of matrix elements).
Processing segments to Xarrays...
Processed 3 sets of DumpIdy file segments, (0 blank)
*** ePSproc readMatEle(): scanning files for CrossSection segments.
*** Scanning file(s)
['D:\\code\\github\\ePSproc\\data\\photoionization\\no2_demo_ePS.out']
*** Reading ePS output file: D:\code\github\ePSproc\data\photoionization\no2_demo_ePS.out
Expecting 1 energy points.
Expecting 3 symmetries.
Scanning CrossSection segments.
Expecting 4 CrossSection segments.
Found 4 CrossSection segments (sets of results).
Processed 4 sets of CrossSection file segments, (0 blank)
[23]:
# Set standard pol geoms (== (z,x,y) as used above)
eAngs = ep.setPolGeoms()
# Calculate for each pol geom
start = time.time()
BLM = ep.mfblmEuler(dataSet[0], selDims=selDims, eAngs = eAngs, thres = thres, SFflag = True, verbose = 0) # Run for all Eke. Note this fails if selDims = None, to fix!
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points, {2} polarisations, threshold={3}.'.format((end-start), BLM.Eke.size, eAngs.size, thres))
# Elapsed time = 314.4399154186249 seconds, for 1 energy points, 3 polarisations, threshold=0.0001.
# NOTE much longer than N2 case (~75s) due to number of matrix elements.
Calculating MFBLMs for 17956 pairs... Eke = 0.81 eV, eAngs = (<xarray.DataArray ()>
array(quaternion(1, -0, 0, 0), dtype=quaternion)
Coordinates:
Euler object (0.0, 0.0, 0.0)
Labels <U18 'z'
Attributes:
dataType: Euler)
Calculating MFBLMs for 17956 pairs... Eke = 0.81 eV, eAngs = (<xarray.DataArray ()>
array(quaternion(0.707106781186548, -0, 0.707106781186548, 0),
dtype=quaternion)
Coordinates:
Euler object (0.0, 1.5707963267948966, 0.0)
Labels <U18 'x'
Attributes:
dataType: Euler)
Calculating MFBLMs for 17956 pairs... Eke = 0.81 eV, eAngs = (<xarray.DataArray ()>
array(quaternion(0.5, -0.5, 0.5, 0.5), dtype=quaternion)
Coordinates:
Euler object (1.5707963267948966, 1.5707963267948966, 0.0)
Labels <U18 'y'
Attributes:
dataType: Euler)
Elapsed time = 314.4399154186249 seconds, for 1 energy points, 3 polarisations, threshold=0.0001.
[41]:
# Full results (before summation)
xDim = 'Labels'
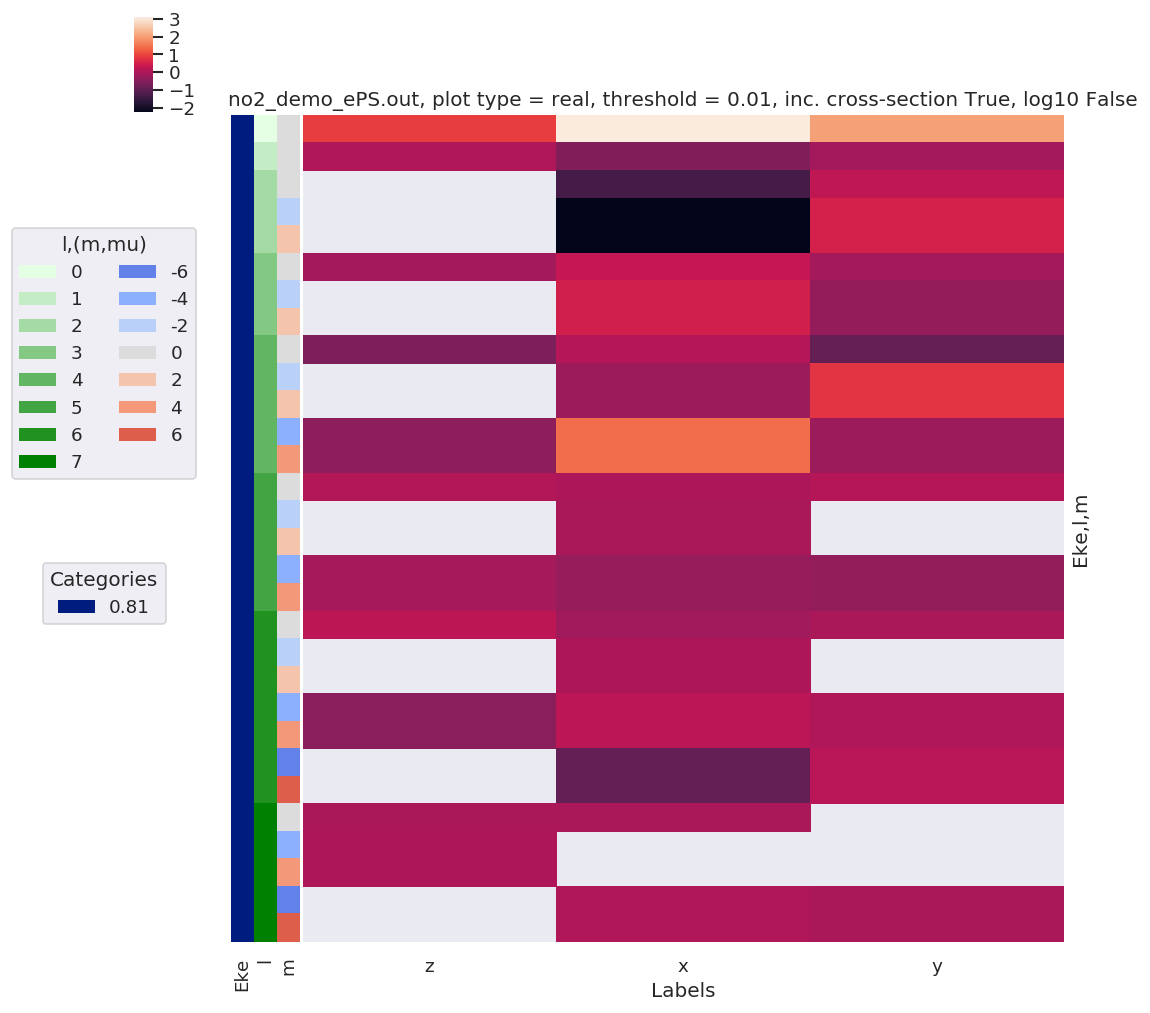
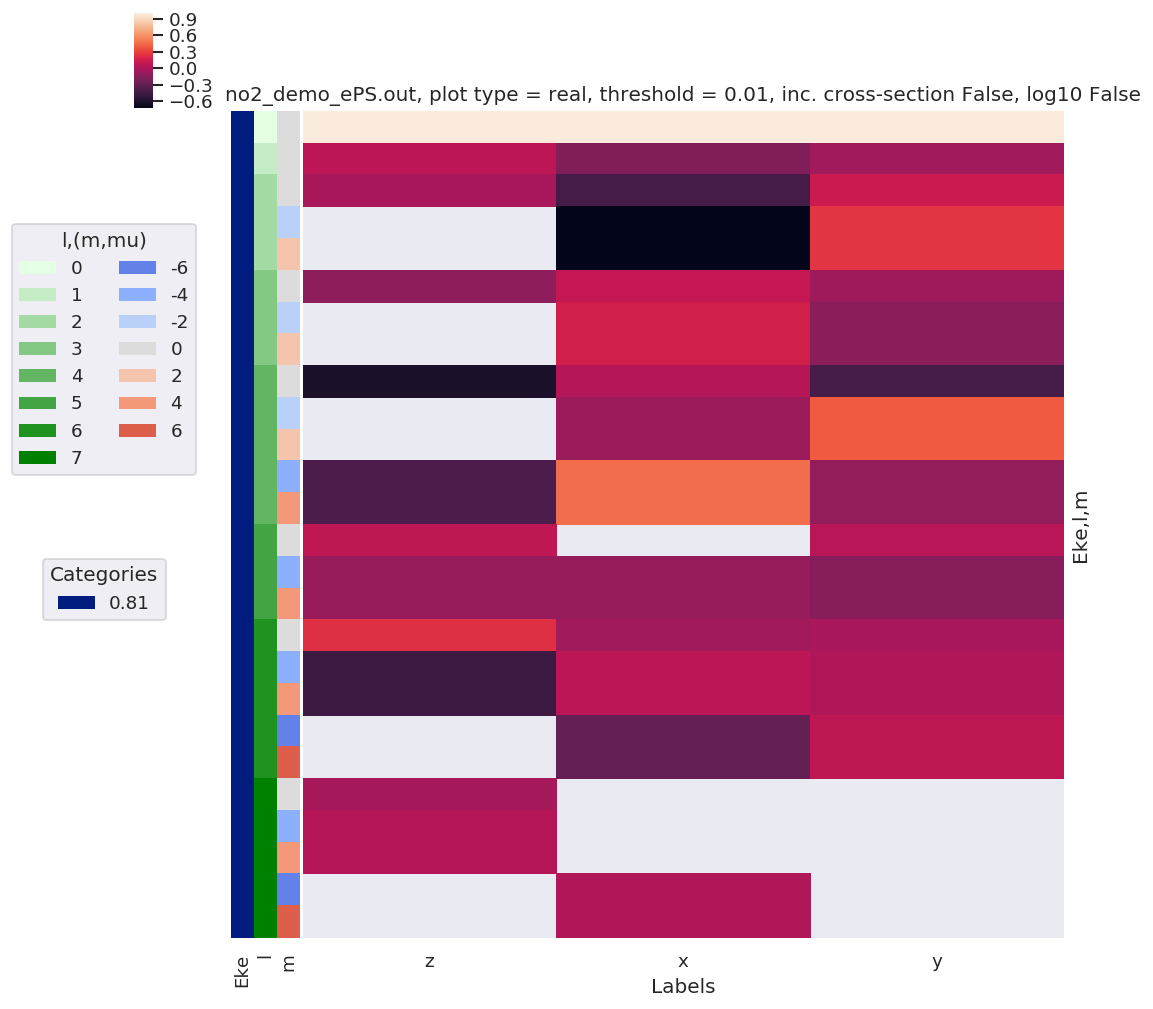
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(BLM.swap_dims({'Euler':'Labels'}), xDim=xDim, sumDims=None, pType = 'r') # Plot values scaled by SF
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(BLM.swap_dims({'Euler':'Labels'}), xDim=xDim, sumDims=None, pType = 'r', SFflag=False) # Plot values with no scaling
Plotting data no2_demo_ePS.out, pType=r, thres=0.01, with Seaborn
Plotting data no2_demo_ePS.out, pType=r, thres=0.01, with Seaborn
[43]:
symSum = True # Sum over symmetry groups, or keep separate?
start = time.time()
mTermST, mTermS, mTermTest = ep.geomFunc.mfblmXprod(dataSet[0], QNs = None, thres = thres, selDims = {'it':1, 'Type':'L'}, thresDims=None, RX=RX, symSum=symSum, SFflag=True, phaseConvention=phaseConvention)
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points, {2} polarizations, threshold={3}.'.format((end-start), mTermST.Eke.size, RX.size, thres))
# Elapsed time = 7.997419357299805 seconds, for 1 energy points, 3 polarizations, threshold=0.0001.
# Note only ~x2 longer than N2 case (3.5s)
Elapsed time = 7.997419357299805 seconds, for 1 energy points, 3 polarizations, threshold=0.0001.
[47]:
# Full results (before summation)
mTermST.attrs['dataType'] = 'matE' # Set matE here to allow for correct plotting of sym dims.
plotDimsRed = ['Labels','L','M'] # Set plotDims to fix dim ordering in plot
if not symSum:
plotDimsRed.extend(['Cont','Targ','Total'])
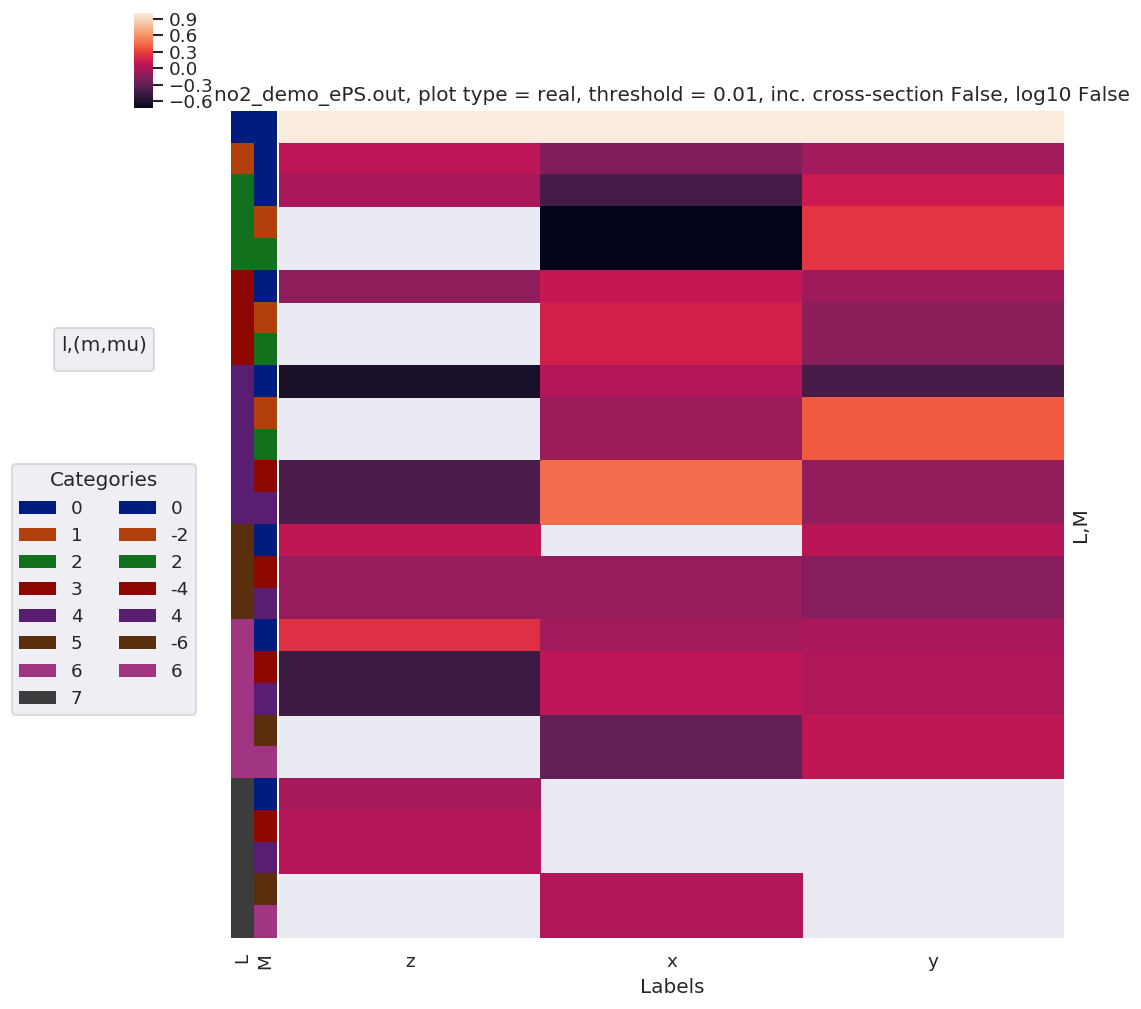
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, xDim=xDim, sumDims=None, pType = 'r', thres = 0.01, fillna = False, SFflag=False)
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True) # If plotDims is not passed use default ordering.
Plotting data no2_demo_ePS.out, pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[61]:
# Confirm subtraction OK
BLMrename = BLM.swap_dims({'Euler':'Labels'}).unstack('BLM').rename({'l':'L','m':'M'}).stack({'LM':['L','M']}) # Reformat Xarray
testSub = (mTermST - BLMrename).squeeze()
testSub.attrs['dataType']='matE'
[62]:
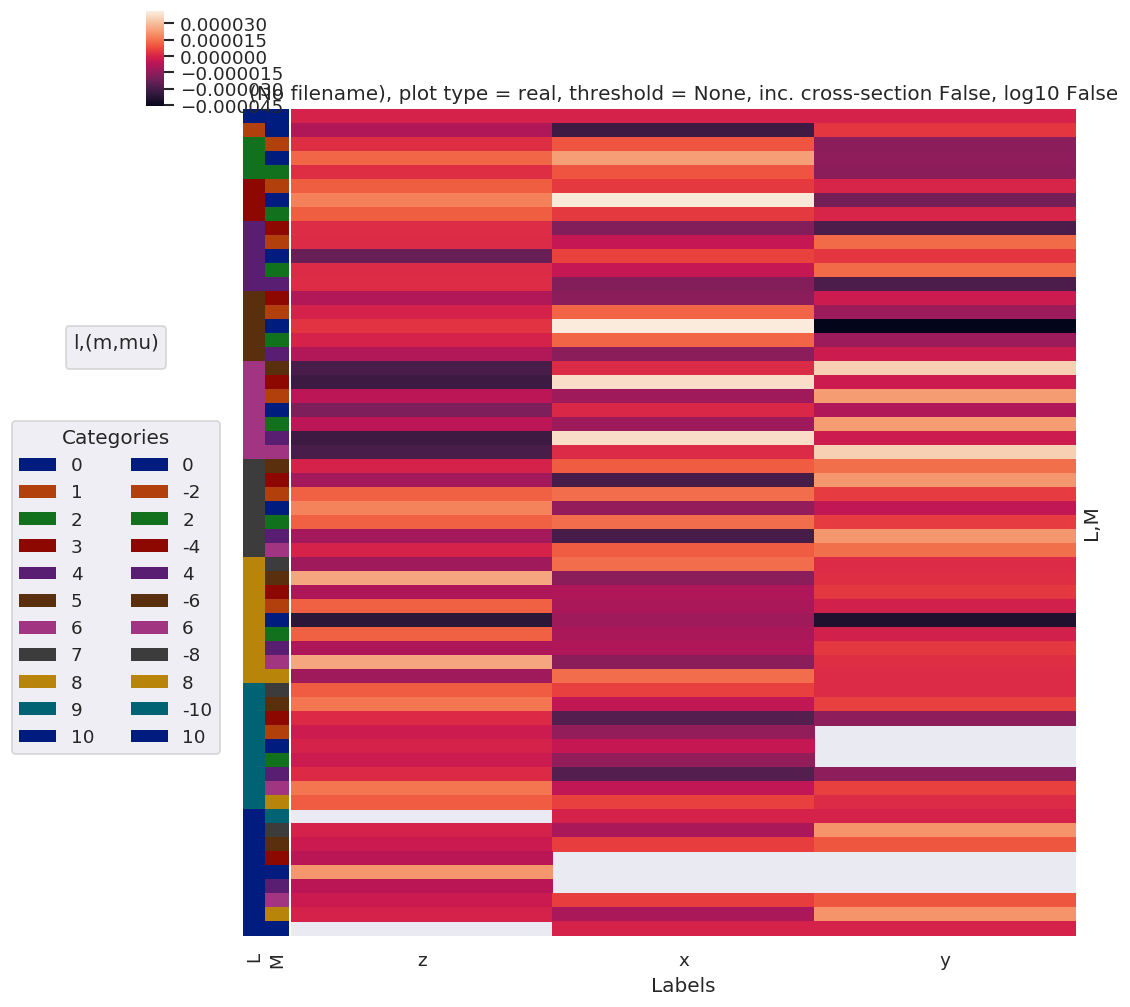
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testSub, xDim=xDim, sumDims=None, pType = 'r', thres = None, fillna = False, SFflag=False)
Plotting data (No filename), pType=r, thres=None, with Seaborn
No handles with labels found to put in legend.
[63]:
print(f"Min difference: {testSub.min().data}, max difference: {testSub.max().data}, threshold: {thres}")
# For thres = 1e-4, max diff = 4e-5
Min difference: (-4.5962933287541086e-05+1.1262398393111875e-17j), max difference: (4.0768195605419937e-05+2.5447083366932985e-23j), threshold: 0.0001
In this case, differences are < threshold, as they should be.
[ ]:
Version info
[64]:
%load_ext version_information
[65]:
%version_information epsproc, xarray
[65]:
| Software | Version |
|---|---|
| Python | 3.7.3 64bit [MSC v.1915 64 bit (AMD64)] |
| IPython | 7.12.0 |
| OS | Windows 10 10.0.18362 SP0 |
| epsproc | 1.2.5-dev |
| xarray | 0.15.0 |
| Tue Apr 14 15:25:37 2020 Eastern Daylight Time | |
[75]:
time.strftime("%a, %d %b %Y %H:%M:%S +0000", time.localtime())
[75]:
'Tue, 14 Apr 2020 15:29:28 +0000'
[ ]: