ePSproc \(\beta_{L,M}\) calculations demo
10/09/19
Source notebook on Github.
Basic IO
[1]:
import sys
import os
import time
import numpy as np
# For module testing, include path to module here
modPath = r'D:\code\github\ePSproc'
sys.path.append(modPath)
import epsproc as ep
* pyevtk not found, VTK export not available.
[2]:
# Load data from modPath\data
dataPath = os.path.join(modPath, 'data')
# Scan data dir
dataSet = ep.readMatEle(fileBase = dataPath)
*** ePSproc readMatEle(): scanning files for DumpIdy segments (matrix elements)
*** Scanning dir
D:\code\github\ePSproc\data
Found 2 .out file(s)
*** Reading ePS output file: D:\code\github\ePSproc\data\n2_3sg_0.1-50.1eV_A2.inp.out
Expecting 51 energy points.
Expecting 2 symmetries.
Expecting 102 dumpIdy segments.
Found 102 dumpIdy segments (sets of matrix elements).
Processing segments to Xarrays...
Processed 102 sets of matrix elements (0 blank)
*** Reading ePS output file: D:\code\github\ePSproc\data\no2_demo_ePS.out
Expecting 1 energy points.
Expecting 3 symmetries.
Expecting 3 dumpIdy segments.
Found 3 dumpIdy segments (sets of matrix elements).
Processing segments to Xarrays...
Processed 3 sets of matrix elements (0 blank)
Formalism
The \(\beta_{L,M}\) parameters are defined as:
$
\begin{eqnarray}
\beta_{L,-M}^{\mu_{i},\mu_{f}} & = & \sum_{l,m,\mu}\sum_{l',m',\mu'}(-1)^{M}(-1)^{m}(-1)^{(\mu'-\mu_{0})}\left(\frac{(2l+1)(2l'+1)(2L+1)}{4\pi}\right)^{1/2}\left(\begin{array}{ccc}
l & l' & L\\
0 & 0 & 0
\end{array}\right)\left(\begin{array}{ccc}
l & l' & L\\
-m & m' & -M
\end{array}\right)\nonumber \\
& \times & \sum_{P,R',R}(2P+1)(-1)^{(R'-R)}\left(\begin{array}{ccc}
1 & 1 & P\\
\mu & -\mu' & R'
\end{array}\right)\left(\begin{array}{ccc}
1 & 1 & P\\
\mu_{0} & -\mu_{0} & R
\end{array}\right)D_{-R',-R}^{P}(R_{\hat{n}})I_{l,m,\mu}^{p_{i}\mu_{i},p_{f}\mu_{f}}(E)I_{l',m',\mu'}^{p_{i}\mu_{i},p_{f}\mu_{f}*}(E)
\end{eqnarray}
$
Calculations use ep.mfblm(), which will calculate all values at each energy point for the supplied dataset. This may take a while in some cases due to multiple nested sums - this code will be parallelised in future.
\(N_2\) mutli-E
Calculate \(\beta_{LM}\) as function of energy.
[3]:
daIn = dataSet[0].copy()
# BLMXeN2 = ep.mfblm(daIn[:, 1:4], selDims = {'Type':'L'}, thres = 1e-4) # Subselected on Eke
start = time.time()
BLMXeN2 = ep.mfblm(daIn, selDims = {'Type':'L'}, thres = 1e-4) # Run for all Eke
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points.'.format((end-start), BLMXeN2.Eke.size))
Calculating MFBLMs for 81 pairs... Eke = 0.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 1.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 2.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 3.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 4.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 5.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 6.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 7.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 8.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 9.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 10.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 11.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 12.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 13.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 14.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 15.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 16.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 17.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 18.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 19.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 20.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 21.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 22.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 23.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 24.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 25.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 26.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 27.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 28.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 29.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 30.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 31.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 32.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 33.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 34.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 35.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 36.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 37.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 38.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 39.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 40.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 41.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 42.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 43.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 44.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 45.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 46.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 47.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 48.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 49.1 eV, eAngs = ([0, 0, 0])
Calculating MFBLMs for 81 pairs... Eke = 50.1 eV, eAngs = ([0, 0, 0])
Elapsed time = 42.335490226745605 seconds, for 51 energy points.
[4]:
BLMXeN2
[4]:
<xarray.DataArray (Euler: 1, Eke: 51, BLM: 121)>
array([[[2.301322 +0.j, 0. +0.j, ..., nan+nanj, nan+nanj],
[2.382333 +0.j, 0. +0.j, ..., nan+nanj, nan+nanj],
...,
[0.092948 +0.j, 0. +0.j, ..., 0. +0.j, 0. +0.j],
[0.095428 +0.j, 0. +0.j, ..., 0. +0.j, 0. +0.j]]])
Coordinates:
* Euler (Euler) MultiIndex
- P (Euler) int64 0
- T (Euler) int64 0
- C (Euler) int64 0
* BLM (BLM) MultiIndex
- l (BLM) int64 0 1 1 1 2 2 2 2 2 3 3 ... 10 10 10 10 10 10 10 10 10 10
- m (BLM) int64 0 -1 0 1 -2 -1 0 1 2 -3 -2 ... 0 1 2 3 4 5 6 7 8 9 10
* Eke (Eke) float64 0.1 1.1 2.1 3.1 4.1 5.1 ... 46.1 47.1 48.1 49.1 50.1
Attributes:
Lmax: 11
Targ: SG
QNs: ['m', 'l', 'mu', 'ip', 'it', 'Value']
dataType: BLM
file: n2_3sg_0.1-50.1eV_A2.inp.out
fileBase: D:\code\github\ePSproc\data
thres: 0.0001
sumDims: ('l', 'm', 'mu', 'Cont', 'Targ', 'Total', 'it')
selDims: [('Type', 'L')]
[5]:
# Plot using Xarray functionality with thresholding
BLMXeN2.where(np.abs(BLMXeN2) > 1e-4, drop = True).real.squeeze().plot.line(x='Eke')
[5]:
[<matplotlib.lines.Line2D at 0x1fd4a9a24a8>,
<matplotlib.lines.Line2D at 0x1fd4a9a2fd0>,
<matplotlib.lines.Line2D at 0x1fd4a9a27b8>,
<matplotlib.lines.Line2D at 0x1fd4b84dc18>,
<matplotlib.lines.Line2D at 0x1fd4b84d940>,
<matplotlib.lines.Line2D at 0x1fd4b84d6a0>]
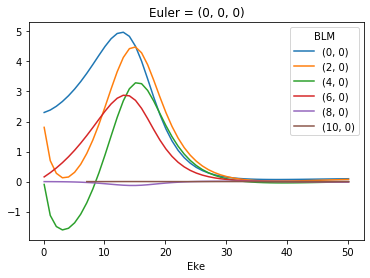
[6]:
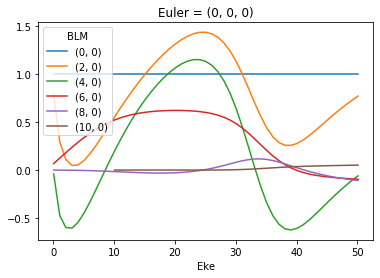
# Plot values normalised by B00
# This seems to work... probably a more elegant solution here, since this assumes dimension order.
normBLM = BLMXeN2/BLMXeN2[:,:,0]
normBLM.where(np.abs(normBLM) > 1e-4, drop = True).real.squeeze().plot.line(x='Eke')
[6]:
[<matplotlib.lines.Line2D at 0x1fd4adb56a0>,
<matplotlib.lines.Line2D at 0x1fd4adb5710>,
<matplotlib.lines.Line2D at 0x1fd4adb5470>,
<matplotlib.lines.Line2D at 0x1fd4adb5668>,
<matplotlib.lines.Line2D at 0x1fd4adb5358>,
<matplotlib.lines.Line2D at 0x1fd4adb5d30>]
MFPADs: calculate & plot from \(\beta_{LM}\)
[7]:
# Calculate & plot MFPADs from BLMs
# def MFPAD_BLM(BLMXin):
# # Calculate YLMs
# YLMX = ep.sphCalc(BLMXin.l.max(), res=50)
# YLMX = YLMX.rename({'LM':'BLM'}) # Switch naming for multiplication & plotting
# MFPAD = BLMXin*YLMX
# MFPAD = MFPAD.rename({'BLM':'LM'})
# return MFPAD
# MFPAD = MFPAD_BLM(BLMXeN2)
MFPAD_N2, _ = ep.sphFromBLMPlot(BLMXeN2)
[8]:
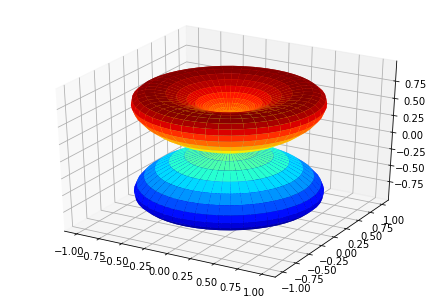
# Plot single E with matplotlib
ep.sphSumPlotX(MFPAD_N2.sel({'Eke':1.1}).squeeze(), pType = 'r', backend = 'mpl')
Plotting with mpl
[8]:
[<Figure size 432x288 with 1 Axes>]
[9]:
# Plot MFPAD surfaces vs E
print('N2 test data, MFPADs vs E')
MFPAD_N2.sum('LM').squeeze().isel(Eke=slice(0,10,2)).real.plot(x='Theta',y='Phi', col='Eke')
N2 test data, MFPADs vs E
[9]:
<xarray.plot.facetgrid.FacetGrid at 0x1fd4b91f048>
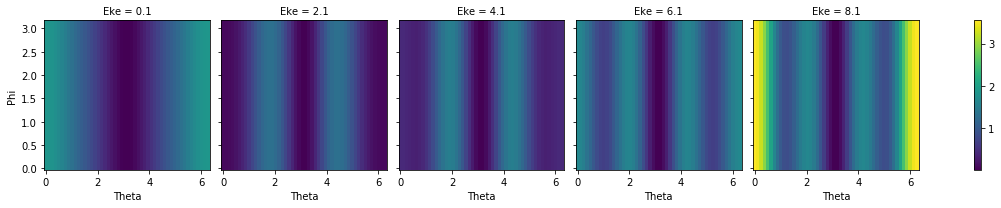
[10]:
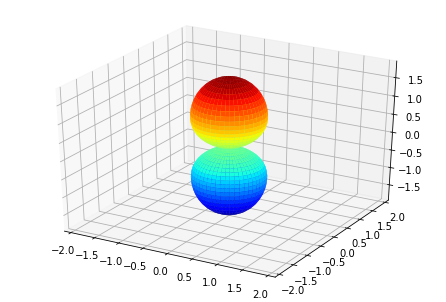
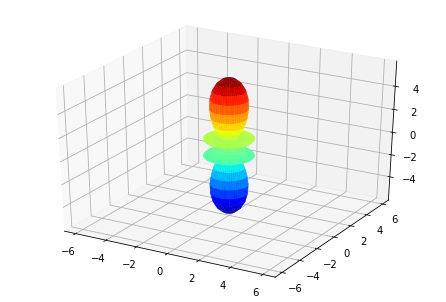
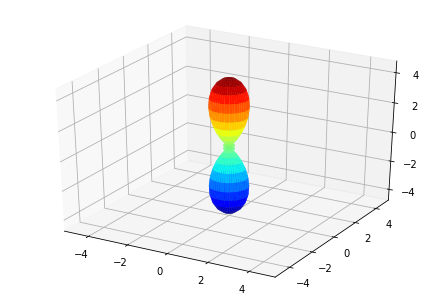
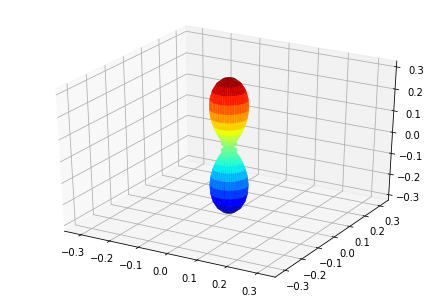
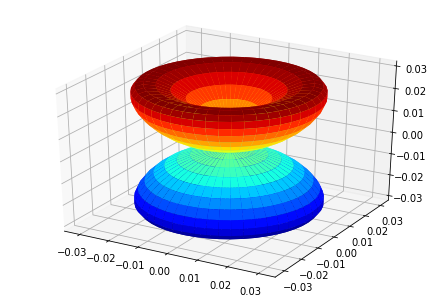
# Plot multiple E with matplotlib
ep.sphSumPlotX(MFPAD_N2.isel(Eke=slice(0,50,10)), pType = 'r', backend = 'mpl')
Plotting with mpl
Data dims: ('Euler', 'Eke', 'Theta', 'Phi'), subplots on Eke
[10]:
[<Figure size 432x288 with 1 Axes>,
<Figure size 432x288 with 1 Axes>,
<Figure size 432x288 with 1 Axes>,
<Figure size 432x288 with 1 Axes>,
<Figure size 432x288 with 1 Axes>]
[11]:
# Plot multiple E with plotly (work in progress!)
# Broken since adding Euler angs...?
_ = ep.sphSumPlotX(MFPAD_N2.squeeze().isel(Eke=slice(0,50,10)), pType = 'r', backend = 'pl')
Plotting with pl
\(NO_2\) (x,y,z) polarizations
Benchmark results, single energy, multiple polarization geometries.
Calculate
[12]:
daIn = dataSet[1].copy()
# Set threshold for matrix elements & BLMs - this can speed up calculations significantly, but will affect accuracy.
thres = 1e-4
# For all pol geoms
pRot = [0, 0, np.pi/2]
tRot = [0, np.pi/2, np.pi/2]
cRot = [0, 0, 0]
eAngs = np.array([pRot, tRot, cRot]).T # List form to use later, rows per set of angles
ts = []
BLMXeNO2list = []
for eIn in range(0,3):
start = time.time()
BLMXeNO2list.append(ep.mfblm(daIn, selDims = {'Type':'L'}, eAngs = eAngs[eIn,:], thres=thres))
ts.append(time.time()-start)
print('Elapsed time = {0} seconds'.format(ts[-1]))
Calculating MFBLMs for 12544 pairs... Eke = 0.81 eV, eAngs = ([0. 0. 0.])
Elapsed time = 124.42453789710999 seconds
Calculating MFBLMs for 12544 pairs... Eke = 0.81 eV, eAngs = ([0. 1.57079633 0. ])
Elapsed time = 126.24425601959229 seconds
Calculating MFBLMs for 12544 pairs... Eke = 0.81 eV, eAngs = ([1.57079633 1.57079633 0. ])
Elapsed time = 125.88551211357117 seconds
[13]:
# Stack results - should improve on this and add eAngs stacking to mfblm code, but OK for testing
import xarray as xr
BLMXeNO2 = xr.combine_nested(BLMXeNO2list,'Euler')
# xr.combine_nested(Tlm, concat_dim=['Euler'])
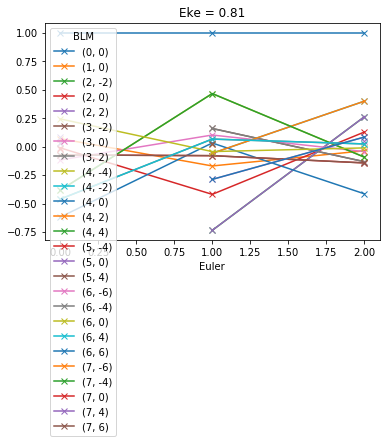
# Plot values normalised by B00
# This seems to work... probably a more elegant solution here, since this assumes dimensions.
normBLM = BLMXeNO2/BLMXeNO2[:,:,0]
# With mag checking to avoid spurious division by small B00 terms...
# normBLM = BLMXeNO2.where(np.abs(BLMXeNO2[:,:,0]) > 1e-4, drop = True)
# normBLM = normBLM/normBLM[:,:,0]
# Replace multi-index with linear index for plotting (otherwise get coord errors)
normBLM['Euler'] = np.arange(0,normBLM.Euler.size)
normBLM.where(np.abs(normBLM) > 1e-2, drop = True).squeeze().real.plot.line('-x',x='Euler')
[13]:
[<matplotlib.lines.Line2D at 0x1fd627882e8>,
<matplotlib.lines.Line2D at 0x1fd62788e80>,
<matplotlib.lines.Line2D at 0x1fd627889b0>,
<matplotlib.lines.Line2D at 0x1fd62788748>,
<matplotlib.lines.Line2D at 0x1fd62788780>,
<matplotlib.lines.Line2D at 0x1fd62788f60>,
<matplotlib.lines.Line2D at 0x1fd62a4bc50>,
<matplotlib.lines.Line2D at 0x1fd62a4b908>,
<matplotlib.lines.Line2D at 0x1fd62a4b5f8>,
<matplotlib.lines.Line2D at 0x1fd62a4b4a8>,
<matplotlib.lines.Line2D at 0x1fd627e5630>,
<matplotlib.lines.Line2D at 0x1fd62a4b278>,
<matplotlib.lines.Line2D at 0x1fd62a4bb70>,
<matplotlib.lines.Line2D at 0x1fd62a4bba8>,
<matplotlib.lines.Line2D at 0x1fd62a4b828>,
<matplotlib.lines.Line2D at 0x1fd62a16048>,
<matplotlib.lines.Line2D at 0x1fd62a16470>,
<matplotlib.lines.Line2D at 0x1fd62a16128>,
<matplotlib.lines.Line2D at 0x1fd62a167f0>,
<matplotlib.lines.Line2D at 0x1fd62a163c8>,
<matplotlib.lines.Line2D at 0x1fd62a169b0>,
<matplotlib.lines.Line2D at 0x1fd62a16c50>,
<matplotlib.lines.Line2D at 0x1fd62a16eb8>,
<matplotlib.lines.Line2D at 0x1fd62a16c88>,
<matplotlib.lines.Line2D at 0x1fd62a16b70>,
<matplotlib.lines.Line2D at 0x1fd62a170f0>]
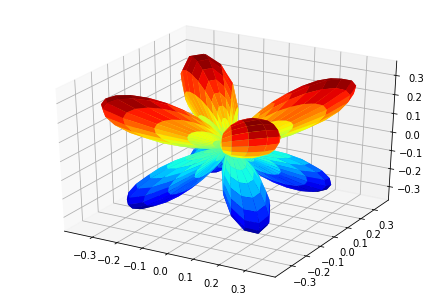
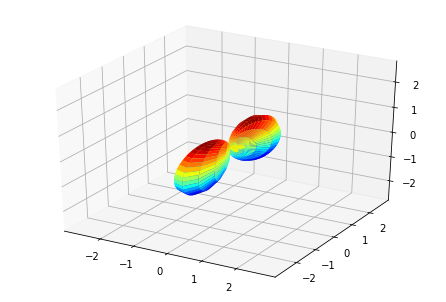
MFPADs
[14]:
MFPAD_NO2, _ = ep.sphFromBLMPlot(BLMXeNO2)
# Plot multiple E with matplotlib
ep.sphSumPlotX(MFPAD_NO2, pType = 'r', backend = 'mpl', facetDim = 'Euler')
Plotting with mpl
Data dims: ('Euler', 'Eke', 'Theta', 'Phi'), subplots on Euler
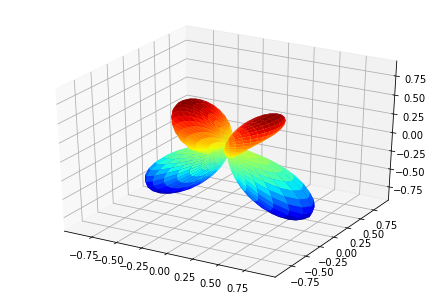
[14]:
[<Figure size 432x288 with 1 Axes>,
<Figure size 432x288 with 1 Axes>,
<Figure size 432x288 with 1 Axes>]
Benchmark vs. “direct” results
Compare against results from ep.mfpad, see main “ePSproc demo notebook” for calculation details.
[15]:
print('MFPADs for test NO2 dataset (single energy, (z,x,y) pol states)')
TX, TlmX = ep.mfpad(dataSet[1])
# Plot for each pol geom (symmetry)
for n in range(0,3):
ep.sphSumPlotX(TX[n].sum('Sym').squeeze()**2, pType = 'a')
MFPADs for test NO2 dataset (single energy, (z,x,y) pol states)
Plotting with mpl
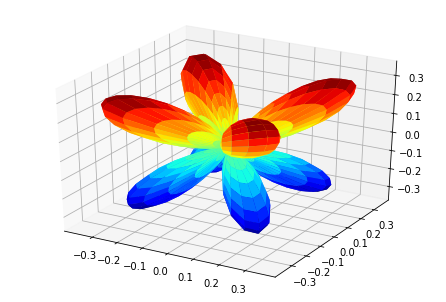
Plotting with mpl
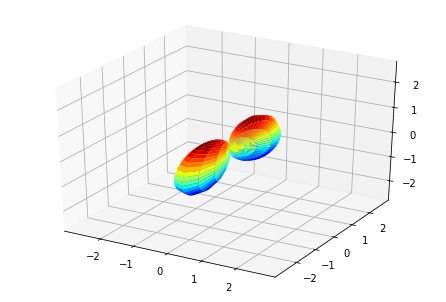
Plotting with mpl
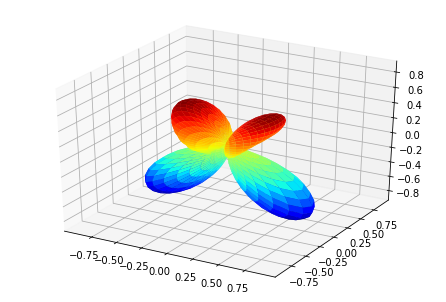
(Visual comparison looks OK, still some benchmarks to to for numerical re/im comparisons, which currently show some differences.)