Method development for geometric functions pt 3: \(\beta\) aligned-frame (AF) parameters with geometric functions.¶
- 01/09/20 v2 with verified AF code.
- 09/06/20 v1
Aims:
- Develop \(\beta_{L,M}\) formalism for AF, using geometric tensor formalism as already applied to MF case.
- Develop corresponding numerical methods - see pt 1 notebook.
- Analyse geometric terms - see pt 1 notebook.
\(\beta_{L,M}^{AF}\) rewrite¶
The various terms defined in pt 1 can be used to redefine the full AF observables, expressed as a set of \(\beta_{L,M}\) coefficients (with the addition of another tensor to define the alignment terms).
The original (full) form for the AF equations, as implemented in ``ePSproc.afblm` <https://epsproc.readthedocs.io/en/dev/modules/epsproc.AFBLM.html>`__ (note, however, that the previous implementation is not fully tested, since it was s…l…o…w… the geometric version should avoid this issue):
Where \(I_{l,m,\mu}^{p_{i}\mu_{i},p_{f}\mu_{f}}(E)\) are the energy-dependent dipole matrix elements, and \(A_{Q,S}^{K}(t)\) define the alignment parameters.
In terms of the geometric parameters, this can be rewritten as:
Where there’s a new alignment tensor:
And the the \(\Lambda_{R',R}\) term is a simplified form of the previously derived MF term:
All phase conventions should be as the MF case, and the numerics for all the ternsors can be used as is… hopefully…
Further notes:
- Note \(B_{L,S-R'}(l,l',m,m')}\) instead of \(B_{L,-M}(l,l',m,m')}\) for MF case. This allows for all MF projections to contribute.
Refs for the full AF-PAD formalism above:
- Reid, Katharine L., and Jonathan G. Underwood. “Extracting Molecular Axis Alignment from Photoelectron Angular Distributions.” The Journal of Chemical Physics 112, no. 8 (2000): 3643. https://doi.org/10.1063/1.480517.
- Underwood, Jonathan G., and Katharine L. Reid. “Time-Resolved Photoelectron Angular Distributions as a Probe of Intramolecular Dynamics: Connecting the Molecular Frame and the Laboratory Frame.” The Journal of Chemical Physics 113, no. 3 (2000): 1067. https://doi.org/10.1063/1.481918.
- Stolow, Albert, and Jonathan G. Underwood. “Time-Resolved Photoelectron Spectroscopy of Non-Adiabatic Dynamics in Polyatomic Molecules.” In Advances in Chemical Physics, edited by Stuart A. Rice, 139:497–584. Advances in Chemical Physics. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2008. https://doi.org/10.1002/9780470259498.ch6.
Where [3] has the version as per the full form above (full asymmetric top alignment distribution expansion).
To consider¶
- Normalisation for ADMs? Will matter in cases where abs cross-sections are valid (but not for PADs generally).
Status¶
- 10/09/20 Now working - see AF/LF verification notebook for more details. May still have function definition issues in some cases?
TODO: more careful comparison with experimental data (see old processing notebooks…)
Setup¶
[1]:
# Imports
import numpy as np
import pandas as pd
import xarray as xr
# Special functions
# from scipy.special import sph_harm
import spherical_functions as sf
import quaternion
# Performance & benchmarking libraries
# from joblib import Memory
# import xyzpy as xyz
import numba as nb
# Timings with ttictoc or time
# https://github.com/hector-sab/ttictoc
from ttictoc import TicToc
import time
# Package fns.
# For module testing, include path to module here
import sys
import os
modPath = r'D:\code\github\ePSproc' # Win test machine
# modPath = r'/home/femtolab/github/ePSproc/' # Linux test machine
sys.path.append(modPath)
import epsproc as ep
# TODO: tidy this up!
from epsproc.util import matEleSelector
from epsproc.geomFunc import geomCalc
* pyevtk not found, VTK export not available.
[2]:
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
[3]:
# Plotters
import matplotlib.pyplot as plt
from epsproc.plot import hvPlotters
hvPlotters.setPlotters()
Alignment terms¶
Axis distribution moments¶
These are already set up by setADMs().
[4]:
# set default alignment terms - single term A(0,0,0)=1, which corresponds to isotropic distributions
AKQS = ep.setADMs()
AKQS
[4]:
<xarray.DataArray (ADM: 1, t: 1)>
array([[1]])
Coordinates:
* ADM (ADM) MultiIndex
- K (ADM) int64 0
- Q (ADM) int64 0
- S (ADM) int64 0
* t (t) int32 0
Attributes:
dataType: ADM[5]:
AKQSpd,_ = ep.util.multiDimXrToPD(AKQS, colDims='t', squeeze=False)
AKQSpd
[5]:
| t | 0 | ||
|---|---|---|---|
| K | Q | S | |
| 0 | 0 | 0 | 1 |
[6]:
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(AKQS, xDim = 't', pType = 'r', squeeze = False) # Note squeeze = False required for 1D case (should add this to code!)
daPlotpd
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[6]:
| t | 0 | ||
|---|---|---|---|
| K | Q | S | |
| 0 | 0 | 0 | 1.0 |
[7]:
# Test multiple t points
AKQS = ep.setADMs(ADMs = [0,0,0,1,1], t=[0,1])
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(AKQS, xDim = 't', pType = 'r', squeeze = False) # Note squeeze = False required for 1D case (should add this to code!)
daPlotpd
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[7]:
| t | 0 | 1 | ||
|---|---|---|---|---|
| K | Q | S | ||
| 0 | 0 | 0 | 1.0 | 1.0 |
[8]:
# Test additional time-dependent values
AKQS = ep.setADMs(ADMs = [[0,0,0,1,1],[2,0,0,0,0.5]], t=[0,1]) # Nested list or np.array OK.
# AKQS = ep.setADMs(ADMs = np.array([[0,0,0,1,1],[2,0,0,0,0.5]]), t=[0,1])
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(AKQS, xDim = 't', pType = 'r', squeeze = False) # Note squeeze = False required for 1D case (should add this to code!)
daPlotpd
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[8]:
| t | 0 | 1 | ||
|---|---|---|---|---|
| K | Q | S | ||
| 0 | 0 | 0 | 1.0 | 1.0 |
| 2 | 0 | 0 | NaN | 0.5 |
Alignment tensor¶
As previously defined:
Function dev¶
Based on existing MF functions, see ep.geomFunc.geomCalc and ep.geomFunc.mfblmGeom.
Most similar to existing betaTerm() function, which also has product of 3j terms in a similar manner.
[9]:
# Generate QNs - code adapted from ep.geomFunc.geomUtils.genllL(Lmin = 0, Lmax = 10, mFlag = True):
# Generate QNs for deltaKQS term - 3j product term
def genKQSterms(Kmin = 0, Kmax = 2, mFlag = True):
# Set QNs for calculation, (l,m,mp)
QNs = []
for P in np.arange(0, 2+1): # HARD-CODED R for testing - should get from EPR tensor defn. in full calcs.
for K in np.arange(Kmin, Kmax+1): # Eventually this will come from alignment term
for L in np.arange(np.abs(P-K), P+K+1): # Allowed L given P and K defined
if mFlag: # Include "m" (or equivalent) terms?
mMax = L
RMax = P
QMax = K
else:
mMax = 0
RMax = 0
QMax = 0
for R in np.arange(-RMax, RMax+1):
for Q in np.arange(-QMax, QMax+1):
#for M in np.arange(np.abs(l-lp), l+lp+1):
# for M in np.arange(-mMax, mMax+1):
# Set M - note this implies specific phase choice.
# M = -(m+mp)
# M = (-m+mp)
# if np.abs(M) <= L: # Skip terms with invalid M
# QNs.append([l, lp, L, m, mp, M])
# Run for all possible M
for M in np.arange(-L, L+1):
QNs.append([P, K, L, R, Q, M])
return np.array(QNs)
# Generate QNs from EPR + AKQS tensors
def genKQStermsFromTensors(EPR, AKQS, uniqueFlag = True, phaseConvention = 'S'):
'''
Generate all QNs for :math:`\Delta_{L,M}(K,Q,S)` from existing tensors (Xarrays) :math:`E_{P,R}` and :math:`A^K_{Q,S}`.
Cf. :py:func:`epsproc.geomFunc.genllpMatE`, code adapted from there.
Parameters
----------
matE : Xarray
Xarray containing matrix elements, with QNs (l,m), as created by :py:func:`readMatEle`
uniqueFlag : bool, default = True
Check for duplicates and remove (can occur with some forms of matrix elements).
mFlag : bool, optional, default = True
m, mp take all passed values if mFlag=True, or =0 only if mFlag=False
phaseConvention : optional, str, default = 'S'
Set phase conventions with :py:func:`epsproc.geomCalc.setPhaseConventions`.
To use preset phase conventions, pass existing dictionary.
If matE.attrs['phaseCons'] is already set, this will be used instead of passed args.
Returns
-------
QNs1, QNs2 : two 2D np.arrays
Values take all allowed combinations ['P','K','L','R','Q','M'] and ['P','K','L','Rp','S','S-Rp'] from supplied matE.
Note phase conventions not applied to QN lists as yet.
To do
-----
- Implement output options (see dev. function w3jTable).
'''
# Local import.
from epsproc.geomFunc.geomCalc import setPhaseConventions
# For transparency/consistency with subfunctions, str/dict now set in setPhaseConventions()
if 'phaseCons' in EPR.attrs.keys():
phaseCons = EPR.attrs['phaseCons']
else:
phaseCons = setPhaseConventions(phaseConvention = phaseConvention)
# Get QNs from inputs
KQScoords = AKQS.unstack().coords # Use unstack here, or np.unique(matE.l), to avoid duplicates
PRcoords = EPR.unstack().coords
# Use passed (m,mp) values, or run for m=mp=0 only.
# if mFlag:
# mList = matE.unstack().m.values
# else:
# mList = 0
# Set QNs for calculation, one set for each 3j term
QNs1 = []
QNs2 = []
for P in PRcoords['P'].values: # Note dictionary syntax for coords objects
for K in KQScoords['K'].values:
for L in np.arange(np.abs(P-K), P+K+1): # Allowed L given P and K defined
# if mFlag: # Include "m" (or equivalent) terms?
# mMax = L
# RMax = P
# QMax = K
# else:
# mMax = 0
# RMax = 0
# QMax = 0
for R in PRcoords['R'].values:
for Q in KQScoords['Q'].values:
# Set M, with +/- phase convention - TBC MAY BE INCORRECT IN THIS CASE/CONTEXT?
# Note that setting phaseCons['afblmCons']['negM'] = phaseCons['genMatEcons']['negm'] is current default case, but doesn't have to be!
if phaseCons['genMatEcons']['negm']:
M = (-R+Q) # Case for M -> -M switch
else:
M = -(R+Q) # Usual phase convention.
if (abs(R)<=P) and (abs(Q)<=K) and (abs(M)<=L): # Check term is valid.
QNs1.append([P, K, L, R, Q, M])
# Set Rp and S - these are essentially independent of R,Q,M, but keep nested for full dim output.
for Rp in PRcoords['R'].values:
for S in KQScoords['S'].values:
if phaseCons['genMatEcons']['negm']:
SRp = (-Rp+S) # Case for M -> -M switch
else:
SRp = -(Rp+S) # Usual phase convention.
# SRp = S-Rp # Set final 3j term, S-Rp
if (abs(Rp)<=P) and (abs(S)<=K) and (abs(SRp)<=L): # Check term is valid.
QNs2.append([P, K, L, Rp, S, SRp])
#for M in np.arange(np.abs(l-lp), l+lp+1):
# for M in np.arange(-mMax, mMax+1):
# Set M - note this implies specific phase choice.
# M = -(m+mp)
# M = (-m+mp)
# if np.abs(M) <= L: # Skip terms with invalid M
# QNs.append([l, lp, L, m, mp, M])
# Run for all possible M
# for M in np.arange(-L, L+1):
# QNs.append([P, K, L, R, Q, M])
if uniqueFlag:
return np.unique(QNs1, axis = 0), np.unique(QNs2, axis = 0)
else:
return np.array(QNs1), np.array(QNs2)
[10]:
test = genKQSterms()
# test.tolist() # Use tolist() to get full array output (not truncated by np)
test.shape
[10]:
(1225, 6)
[11]:
# Can also just use existing fn.
test2 = ep.geomFunc.genllL(Lmax=2)
test2.shape
[11]:
(1225, 6)
[12]:
# Also QN list fn - checks and removes duplicates
QNs = ep.geomFunc.genllL(Lmax=2)
test3 = ep.geomFunc.geomUtils.genllLList(QNs, uniqueFlag = True, mFlag = True)
test3.shape
[12]:
(1225, 6)
All QNs¶
[13]:
# Then calc 3js.... as per betaTerm
form = 'xdaLM' # xds
dlist1 = ['P', 'K', 'L', 'R', 'Q', 'M']
dlist2 = ['P', 'K', 'L', 'Rp', 'S', 'S-Rp']
QNs = ep.geomFunc.genllL(Lmax=2)
[14]:
# Set phase conventions for this case, extending existing structure
phaseCons = ep.geomFunc.setPhaseConventions('E')
phaseCons['afblmCons'] = {}
# (+/-)M phase selection, set as per existing code, betaCons['negM'] = genMatEcons['negm'] # Use -M term in 3j? Should be anti-correlated with genMatEcons['negm']...? 31/03/20 NOW correlated with mfblmCons['Mphase']
# Note this is correlated with QN generation in genllpMatE() - should set equivalent fn for alignment terms.
# In existing case this arises from M = (-m+mp) or M = -(m+mp) choice.
phaseCons['afblmCons']['negM'] = phaseCons['genMatEcons']['negm']
phaseCons['afblmCons']['negQ'] = True
phaseCons['afblmCons']['negS'] = True
# Apply phase conventions to input QNs
# if phaseCons['mfblmCons']['BLMmPhase']:
# QNsBLMtable[:,3] *= -1
# QNsBLMtable[:,5] *= -1
[15]:
# Calculate two 3j terms, with respective QN sets
thrj1 = ep.geomFunc.w3jTable(QNs = QNs, nonzeroFlag = True, form = form, dlist = dlist1)
thrj2 = ep.geomFunc.w3jTable(QNs = QNs, nonzeroFlag = True, form = form, dlist = dlist2)
[16]:
# Multiplication term...
testMult = thrj1.unstack() * thrj2.unstack()
# This can get large quickly - for Kmax=2 already have 2e6 terms
[17]:
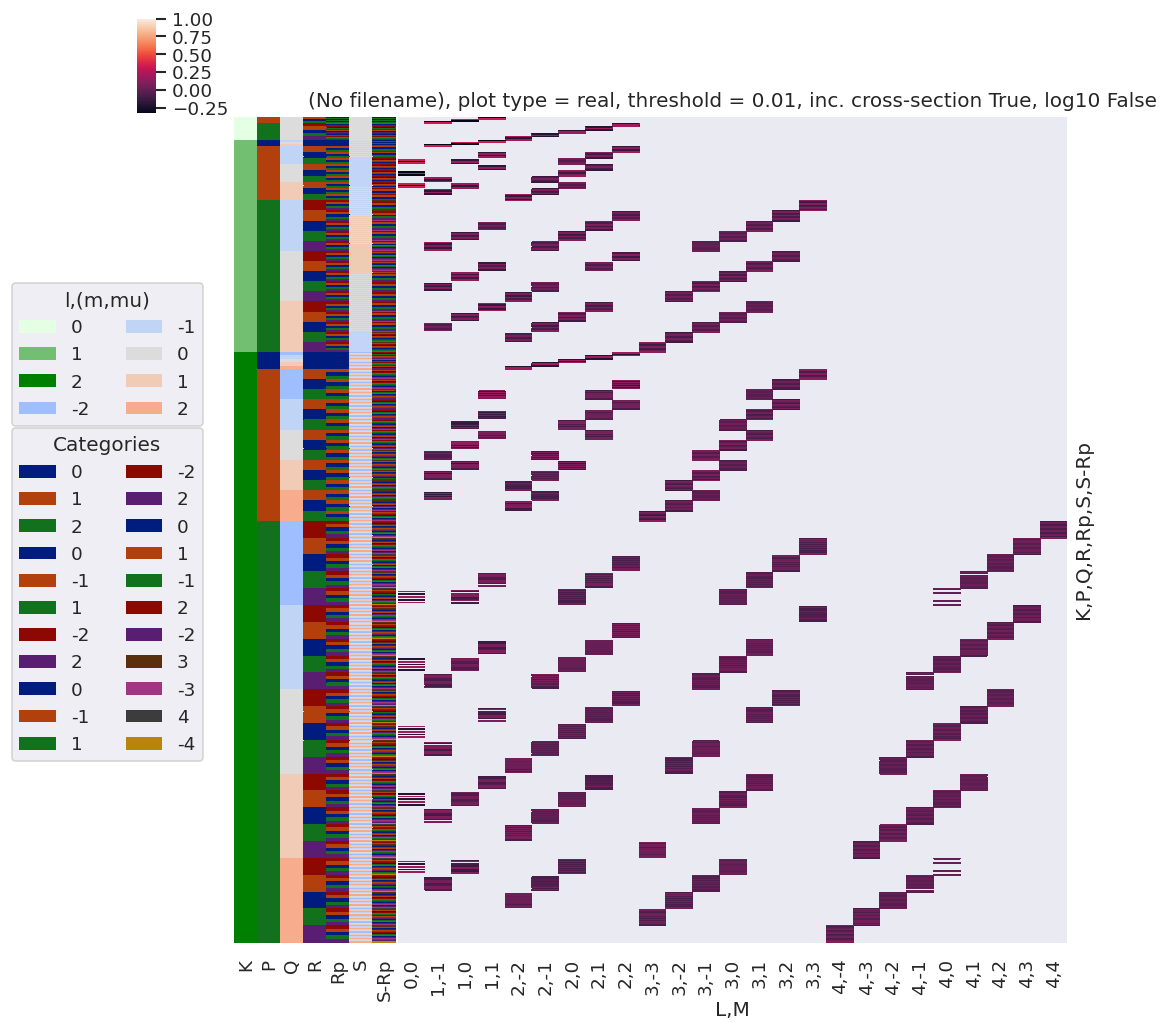
# plotDimsRed = ['l', 'm', 'lp', 'mp']
xDim = {'LM':['L','M']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, xDim=xDim, pType = 'r')
Set dataType (No dataType)
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\core\nputils.py:215: RuntimeWarning:
All-NaN slice encountered
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
Reduced QNs set¶
[18]:
# Then calc 3js.... as per betaTerm
form = 'xdaLM' # xds
dlist1 = ['P', 'K', 'L', 'R', 'Q', 'M']
dlist2 = ['P', 'K', 'L', 'Rp', 'S', 'S-Rp']
# Calculate two 3j terms, with respective QN sets
thrj1 = ep.geomFunc.w3jTable(QNs = QNs, nonzeroFlag = True, form = form, dlist = dlist1)
thrj2 = ep.geomFunc.w3jTable(QNs = QNs, nonzeroFlag = True, form = form, dlist = dlist2)
[19]:
# With subselection (currently don't have QN generation fnc of correct form - see geomUtils)
# from epsproc.util import matEleSelector
# thrj1Sel = ep.util.matEleSelector(thrj1, inds = {'Q':0}, sq=False)
[20]:
# Check 3j terms
xDim = {'LM':['L','M']}
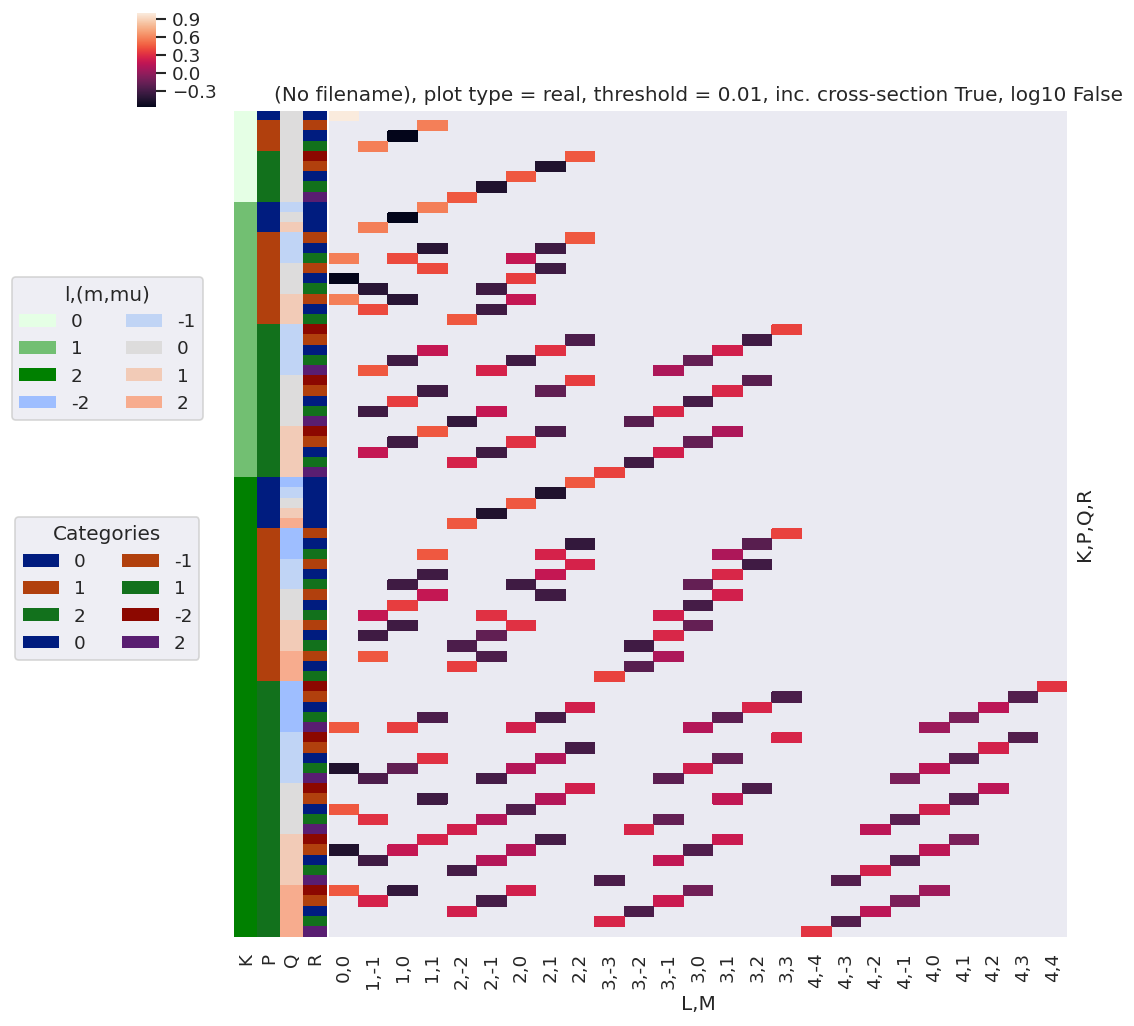
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(thrj1, xDim=xDim, pType = 'r')
xDim = {'LM':['L','S-Rp']}
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(thrj2.sel({'S':0}), xDim=xDim, pType = 'r')
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\core\nputils.py:215: RuntimeWarning:
All-NaN slice encountered
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\core\nputils.py:215: RuntimeWarning:
All-NaN slice encountered
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
[21]:
# Multiplication term...
testMultSub = thrj1.unstack().sel({'Q':0}) * thrj2.unstack().sel({'S':0}) # SLOW, 91125 elements. ACTUALLY - much faster after a reboot. Sigh.
testMultSub2 = thrj1.sel({'Q':0}).unstack() * thrj2.sel({'S':0}).unstack() # FAST, 28125 elements. Possible issue with which dims are dropped - check previous notes!
# This can get large quickly - for Kmax=2 already have 2e6 terms
testMultSub.notnull().sum() # == 194 for Kmax = 2, Q=S=0
testMultSub2.notnull().sum() # == 194 for Kmax = 2, Q=S=0 OK
[21]:
<xarray.DataArray 'w3jStacked' ()>
array(194)
Coordinates:
Q int64 0
S int64 0[21]:
<xarray.DataArray 'w3jStacked' ()> array(194)
[22]:
# plotDimsRed = ['l', 'm', 'lp', 'mp']
xDim = {'LM':['L','M']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
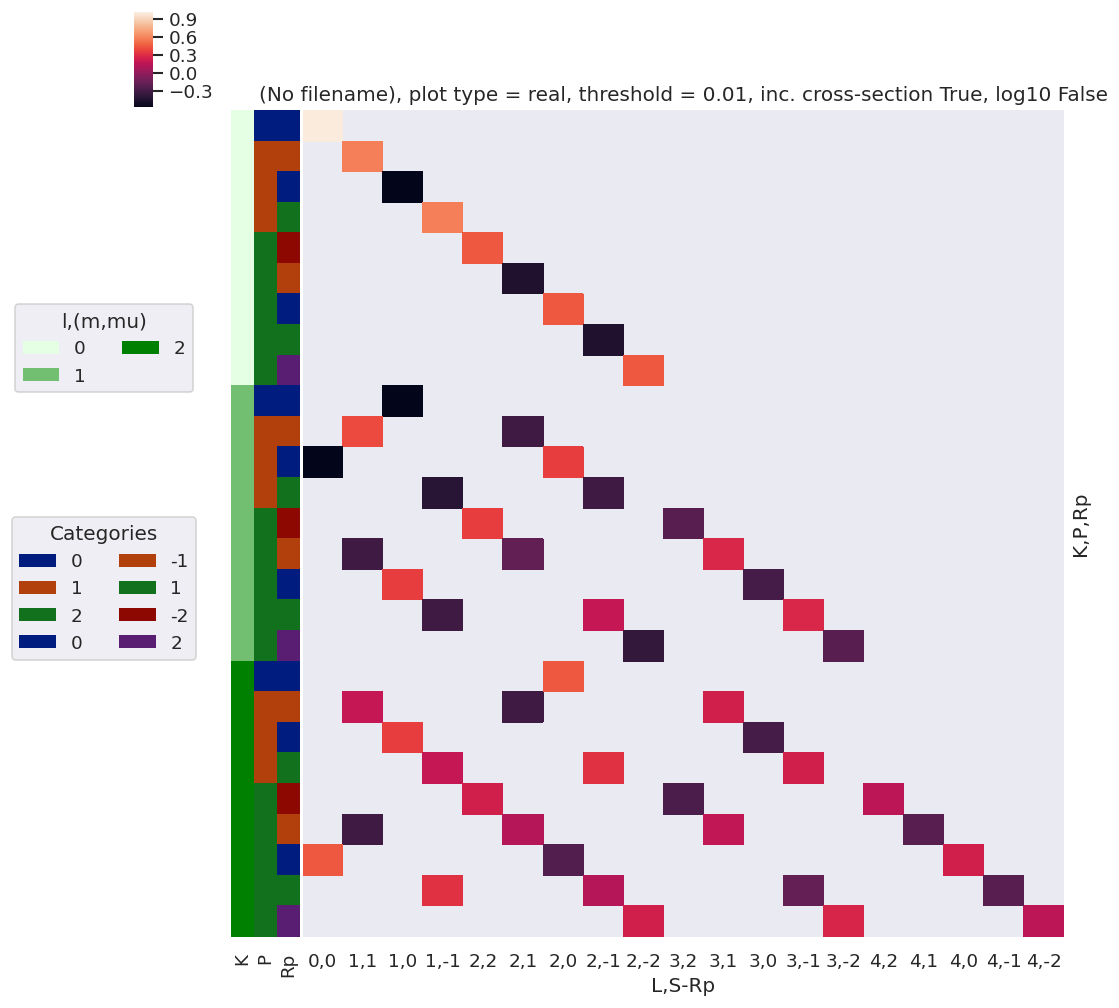
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMultSub, xDim=xDim, pType = 'r')
Set dataType (No dataType)
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\core\nputils.py:215: RuntimeWarning:
All-NaN slice encountered
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
[23]:
# plotDimsRed = ['l', 'm', 'lp', 'mp']
xDim = {'LM':['L','M']}
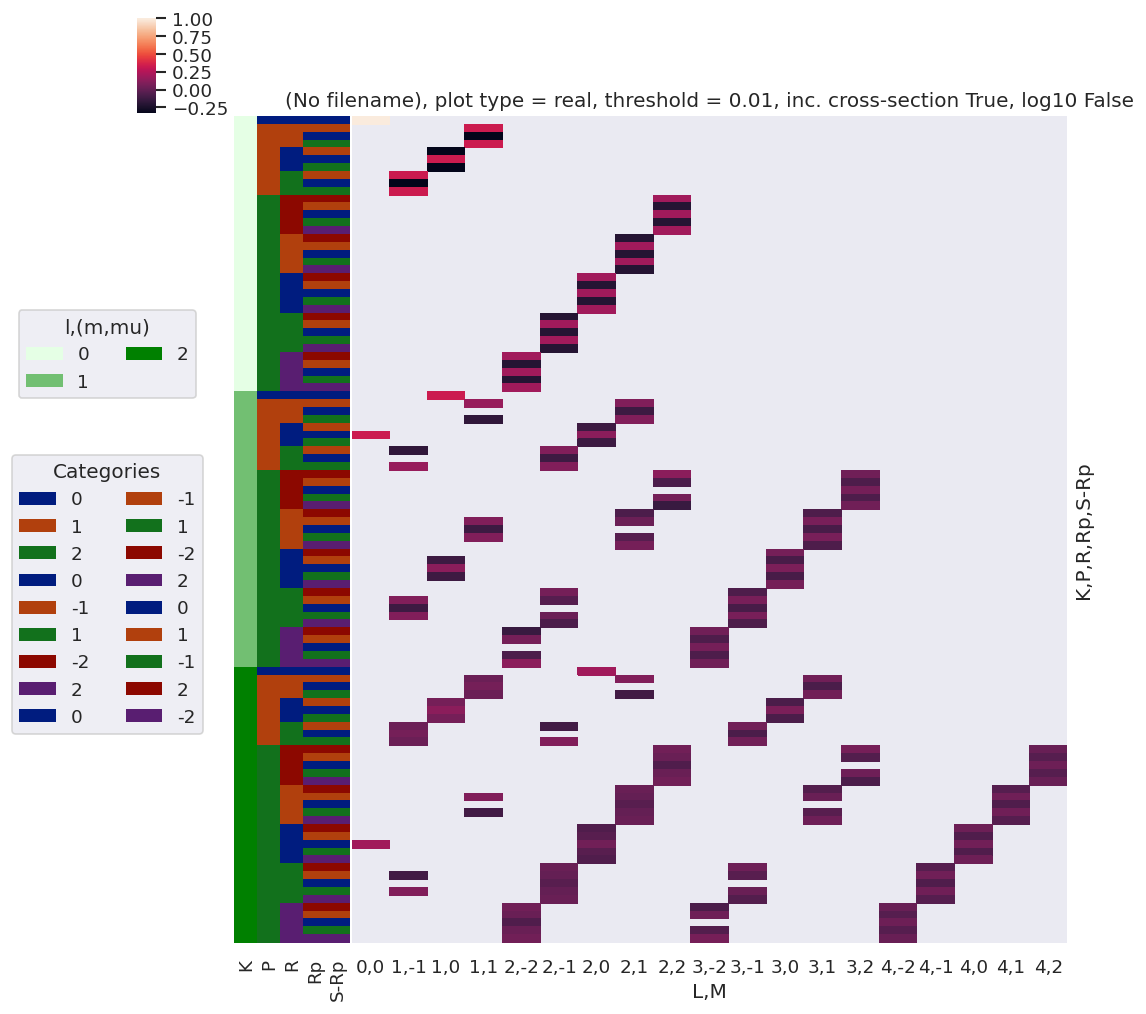
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMultSub2, xDim=xDim, pType = 'r')
Set dataType (No dataType)
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\core\nputils.py:215: RuntimeWarning:
All-NaN slice encountered
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
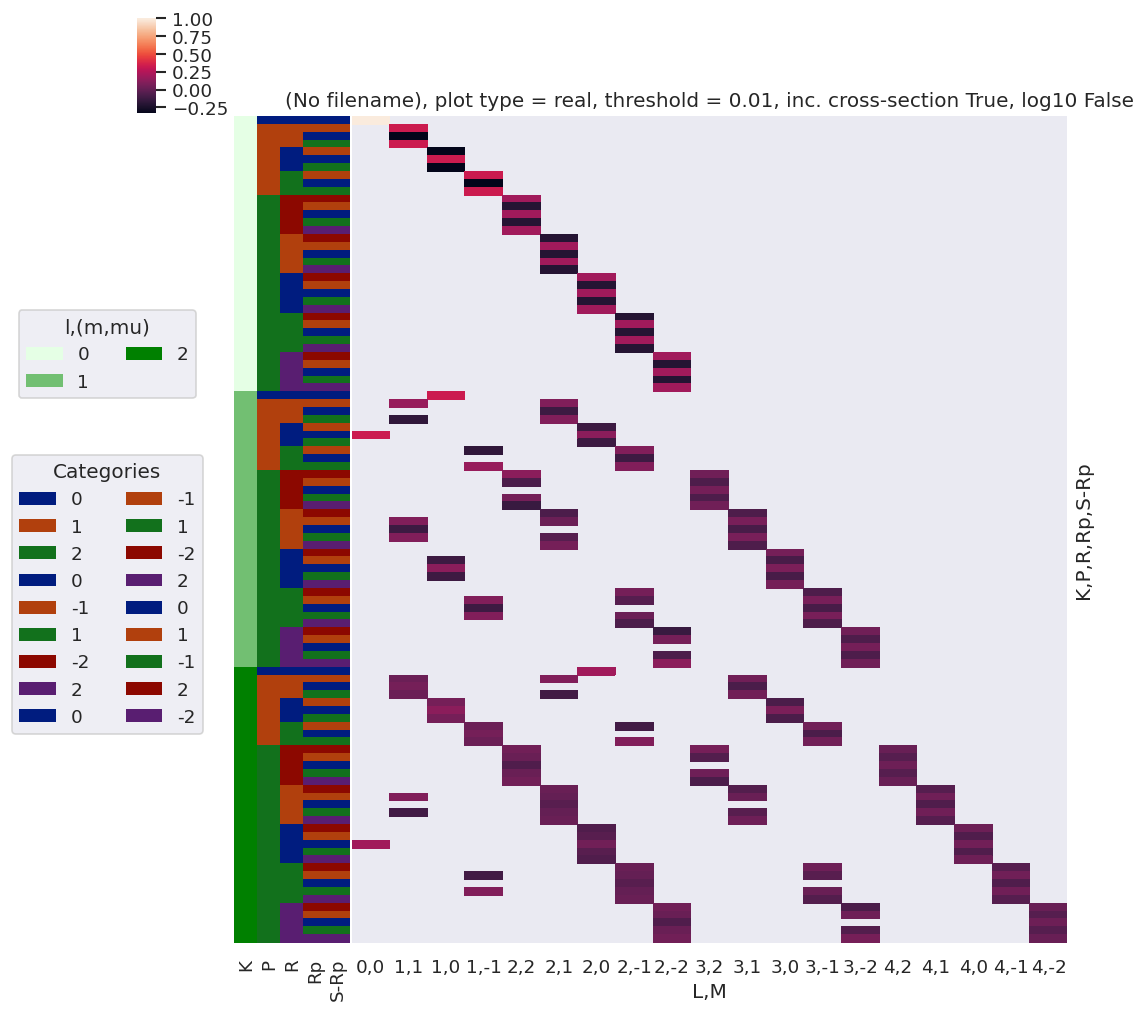
Plots appear to be the same, aside from ordering of M terms(?)
QNs from existing tensors¶
[24]:
phaseConvention = 'E'
# Set polarisation term
p=[0]
EPRX = geomCalc.EPR(form = 'xarray', p = p, nonzeroFlag = True, phaseConvention = phaseConvention).unstack().sel({'R-p':0}).drop('R-p') # Set for R-p = 0 for p=0 case (redundant coord) - need to fix in e-field mult term!
EPRXresort = EPRX.squeeze(['l','lp']).drop(['l','lp']) # Safe squeeze & drop of selected singleton dims only.
# Set alignment terms (inc. time-dependence)
AKQS = ep.setADMs(ADMs = [[0,0,0,1,1],[2,0,0,0,0.5]], t=[0,1]) # Nested list or np.array OK.
[25]:
# Calculate alignment term - this cell should form core function, cf. betaTerm() etc.
# Set QNs
QNs1, QNs2 = genKQStermsFromTensors(EPRXresort, AKQS, uniqueFlag = True, phaseConvention = phaseConvention)
# Then calc 3js.... as per betaTerm
form = 'xdaLM' # xds
dlist1 = ['P', 'K', 'L', 'R', 'Q', 'M']
dlist2 = ['P', 'K', 'L', 'Rp', 'S', 'S-Rp']
# Copy QNs and apply any additional phase conventions
QNs1DeltaTable = QNs1.copy()
QNs2DeltaTable = QNs2.copy()
# Set additional phase cons here - these will be set in master function eventually!
# NOTE - only testing for Q=S=0 case initially.
phaseCons['afblmCons']['negM'] = phaseCons['genMatEcons']['negm'] # IF SET TO TRUE THIS KNOCKS OUT M!=0 terms - not sure if this is correct here, depends also on phase cons in genKQStermsFromTensors().
# Yeah, looks like phase error in current case, get terms with R=M, instead of R=-M
# Confusion is due to explicit assignment of +/-M terms in QN generation (only allowed terms), which *already* enforces this phase convention.
phaseCons['afblmCons']['negQ'] = True
phaseCons['afblmCons']['negS'] = True
# Switch signs (m,M) before 3j calcs.
if phaseCons['afblmCons']['negQ']:
QNs1DeltaTable[:,4] *= -1
# Switch sign Q > -Q before 3j calcs.
if phaseCons['afblmCons']['negM']:
QNs1DeltaTable[:,5] *= -1
# Switch sign S > -S before 3j calcs.
if phaseCons['afblmCons']['negS']:
QNs2DeltaTable[:,4] *= -1
# Calculate two 3j terms, with respective QN sets
thrj1 = ep.geomFunc.w3jTable(QNs = QNs1DeltaTable, nonzeroFlag = True, form = form, dlist = dlist1)
thrj2 = ep.geomFunc.w3jTable(QNs = QNs2DeltaTable, nonzeroFlag = True, form = form, dlist = dlist2)
# Multiply
thrjMult = thrj1.unstack() * thrj2.unstack()
# Additional terms & multiplications
Kdegen = np.sqrt(2*thrjMult.K + 1)
KQphase = np.power(-1, np.abs(thrjMult.K + thrjMult.Q))
DeltaKQS = Kdegen * KQphase * thrjMult
# AF term
AFterm = (DeltaKQS * AKQS.unstack()).sum({'K','Q','S'})
[26]:
thrjMult.notnull().sum() # == 69 for test case with all phase switches on, and same for no phase switches (in test case Q=S=0 in any case!)
[26]:
<xarray.DataArray 'w3jStacked' ()> array(69)
[27]:
# Plot
xDim = {'LM':['L','M']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(DeltaKQS, xDim=xDim, pType = 'r')
daPlotpd
Set dataType (No dataType)
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\core\nputils.py:215: RuntimeWarning:
All-NaN slice encountered
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
[27]:
| L | 0 | 1 | 2 | 3 | 4 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | ||||||
| K | P | Q | R | Rp | S | S-Rp | |||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.000000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 1 | 0 | -1 | -1 | 0 | 1 | NaN | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 0 | 0 | 0 | NaN | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 0 | -1 | 0 | 1 | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 0 | 0 | 0 | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | -1 | 0 | 1 | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 0 | 0 | 0 | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 2 | 0 | -1 | -1 | 0 | 1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | |
| 0 | 0 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | -0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 0 | -1 | 0 | 1 | NaN | NaN | NaN | NaN | NaN | -0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 0 | 0 | 0 | NaN | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | NaN | NaN | NaN | NaN | -0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | -1 | 0 | 1 | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 0 | 0 | 0 | NaN | NaN | NaN | NaN | -0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | NaN | NaN | NaN | NaN | NaN | 0.447214 | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 1 | 0 | -1 | -1 | 0 | 1 | NaN | NaN | NaN | 0.074536 | NaN | NaN | 0.223607 | NaN | NaN | 0.127775 | NaN | NaN | NaN | |
| 0 | 0 | 0 | NaN | NaN | NaN | 0.149071 | NaN | NaN | NaN | NaN | NaN | -0.156492 | NaN | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | NaN | NaN | 0.074536 | NaN | NaN | -0.223607 | NaN | NaN | 0.127775 | NaN | NaN | NaN | ||||
| 0 | -1 | 0 | 1 | NaN | NaN | 0.149071 | NaN | NaN | NaN | NaN | NaN | -0.156492 | NaN | NaN | NaN | NaN | |||
| 0 | 0 | 0 | NaN | NaN | 0.298142 | NaN | NaN | NaN | NaN | NaN | 0.191663 | NaN | NaN | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | NaN | 0.149071 | NaN | NaN | NaN | NaN | NaN | -0.156492 | NaN | NaN | NaN | NaN | ||||
| 1 | -1 | 0 | 1 | NaN | 0.074536 | NaN | NaN | -0.223607 | NaN | NaN | 0.127775 | NaN | NaN | NaN | NaN | NaN | |||
| 0 | 0 | 0 | NaN | 0.149071 | NaN | NaN | NaN | NaN | NaN | -0.156492 | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | 0.074536 | NaN | NaN | 0.223607 | NaN | NaN | 0.127775 | NaN | NaN | NaN | NaN | NaN | ||||
| 2 | 0 | -1 | -1 | 0 | 1 | NaN | NaN | NaN | 0.223607 | NaN | NaN | 0.031944 | NaN | NaN | 0.063888 | NaN | NaN | 0.106479 | |
| 0 | 0 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | -0.063888 | NaN | NaN | NaN | NaN | NaN | -0.116642 | ||||
| 1 | 0 | -1 | NaN | NaN | NaN | -0.223607 | NaN | NaN | 0.031944 | NaN | NaN | -0.063888 | NaN | NaN | 0.106479 | ||||
| 0 | -1 | 0 | 1 | NaN | NaN | NaN | NaN | NaN | -0.063888 | NaN | NaN | NaN | NaN | NaN | -0.116642 | NaN | |||
| 0 | 0 | 0 | 0.447214 | NaN | NaN | NaN | NaN | 0.127775 | NaN | NaN | NaN | NaN | NaN | 0.127775 | NaN | ||||
| 1 | 0 | -1 | NaN | NaN | NaN | NaN | NaN | -0.063888 | NaN | NaN | NaN | NaN | NaN | -0.116642 | NaN | ||||
| 1 | -1 | 0 | 1 | NaN | -0.223607 | NaN | NaN | 0.031944 | NaN | NaN | -0.063888 | NaN | NaN | 0.106479 | NaN | NaN | |||
| 0 | 0 | 0 | NaN | NaN | NaN | NaN | -0.063888 | NaN | NaN | NaN | NaN | NaN | -0.116642 | NaN | NaN | ||||
| 1 | 0 | -1 | NaN | 0.223607 | NaN | NaN | 0.031944 | NaN | NaN | 0.063888 | NaN | NaN | 0.106479 | NaN | NaN | ||||
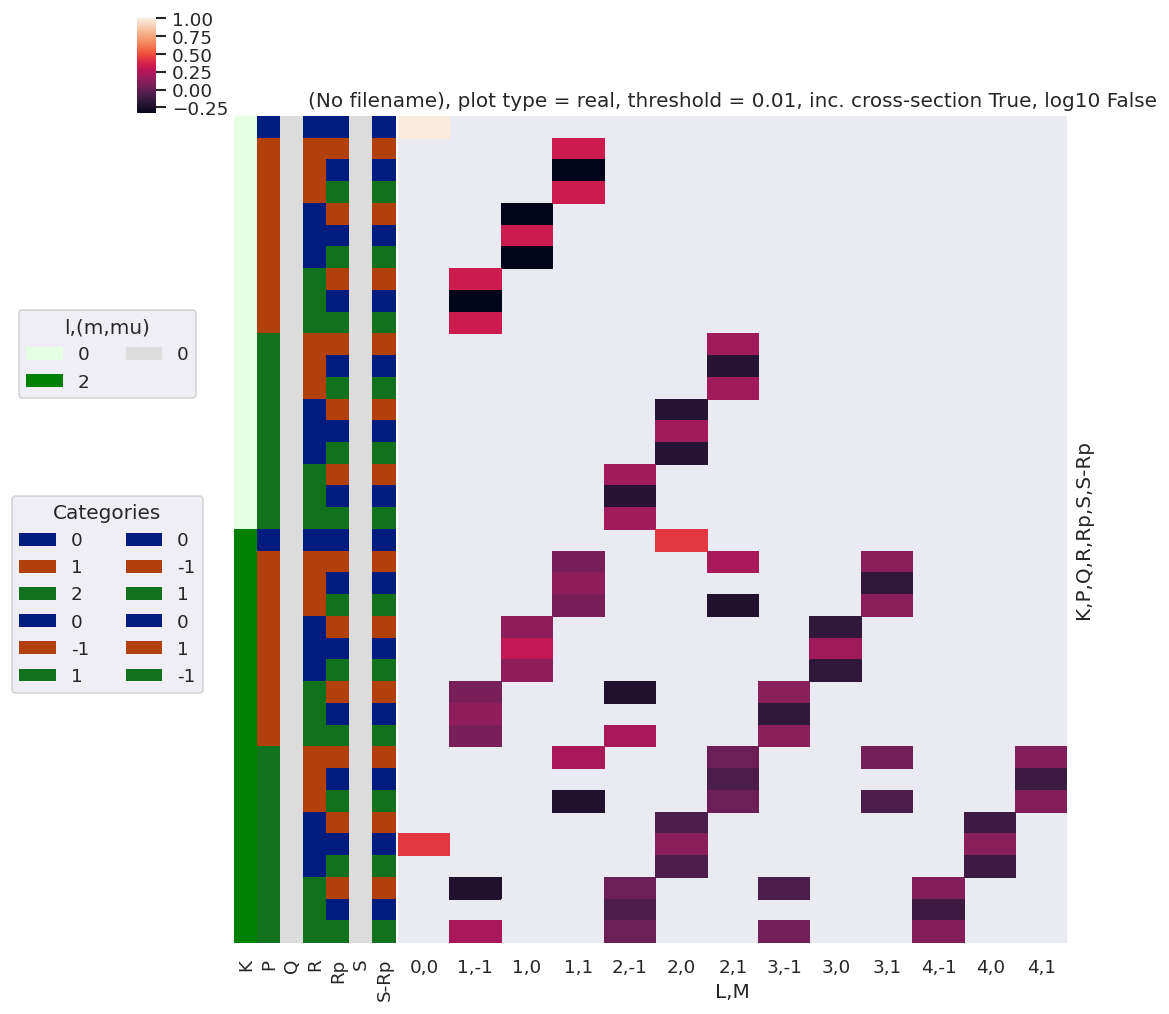
[28]:
# Plot
xDim = {'LM':['L','M']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(AFterm, xDim=xDim, pType = 'r')
daPlotpd
Set dataType (No dataType)
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[28]:
| L | 0 | 1 | 2 | 3 | 4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | ||||
| P | R | Rp | S-Rp | t | |||||||||||||
| 0 | 0 | 0 | 0 | 0 | 1.000000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 1 | 1.000000 | NaN | NaN | NaN | NaN | 0.223607 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | -1 | -1 | 1 | 0 | NaN | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 1 | NaN | NaN | NaN | 0.370601 | NaN | NaN | 0.111803 | NaN | NaN | 0.063888 | NaN | NaN | NaN | ||||
| 0 | 0 | 0 | NaN | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | -0.258798 | NaN | NaN | NaN | NaN | NaN | -0.078246 | NaN | NaN | NaN | ||||
| 1 | -1 | 0 | NaN | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | 0.370601 | NaN | NaN | -0.111803 | NaN | NaN | 0.063888 | NaN | NaN | NaN | ||||
| 0 | -1 | 1 | 0 | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 1 | NaN | NaN | -0.258798 | NaN | NaN | NaN | NaN | NaN | -0.078246 | NaN | NaN | NaN | NaN | ||||
| 0 | 0 | 0 | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | NaN | 0.482405 | NaN | NaN | NaN | NaN | NaN | 0.095831 | NaN | NaN | NaN | NaN | ||||
| 1 | -1 | 0 | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | NaN | -0.258798 | NaN | NaN | NaN | NaN | NaN | -0.078246 | NaN | NaN | NaN | NaN | ||||
| 1 | -1 | 1 | 0 | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 1 | NaN | 0.370601 | NaN | NaN | -0.111803 | NaN | NaN | 0.063888 | NaN | NaN | NaN | NaN | NaN | ||||
| 0 | 0 | 0 | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | -0.258798 | NaN | NaN | NaN | NaN | NaN | -0.078246 | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | -1 | 0 | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | 0.370601 | NaN | NaN | 0.111803 | NaN | NaN | 0.063888 | NaN | NaN | NaN | NaN | NaN | ||||
| 2 | -1 | -1 | 1 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN |
| 1 | NaN | NaN | NaN | 0.111803 | NaN | NaN | 0.215972 | NaN | NaN | 0.031944 | NaN | NaN | 0.053240 | ||||
| 0 | 0 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | -0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | NaN | NaN | -0.231944 | NaN | NaN | NaN | NaN | NaN | -0.058321 | ||||
| 1 | -1 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | -0.111803 | NaN | NaN | 0.215972 | NaN | NaN | -0.031944 | NaN | NaN | 0.053240 | ||||
| 0 | -1 | 1 | 0 | NaN | NaN | NaN | NaN | NaN | -0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 1 | NaN | NaN | NaN | NaN | NaN | -0.231944 | NaN | NaN | NaN | NaN | NaN | -0.058321 | NaN | ||||
| 0 | 0 | 0 | NaN | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | 0.223607 | NaN | NaN | NaN | NaN | 0.263888 | NaN | NaN | NaN | NaN | NaN | 0.063888 | NaN | ||||
| 1 | -1 | 0 | NaN | NaN | NaN | NaN | NaN | -0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | NaN | -0.231944 | NaN | NaN | NaN | NaN | NaN | -0.058321 | NaN | ||||
| 1 | -1 | 1 | 0 | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 1 | NaN | -0.111803 | NaN | NaN | 0.215972 | NaN | NaN | -0.031944 | NaN | NaN | 0.053240 | NaN | NaN | ||||
| 0 | 0 | 0 | NaN | NaN | NaN | NaN | -0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | -0.231944 | NaN | NaN | NaN | NaN | NaN | -0.058321 | NaN | NaN | ||||
| 1 | -1 | 0 | NaN | NaN | NaN | NaN | 0.200000 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 1 | NaN | 0.111803 | NaN | NaN | 0.215972 | NaN | NaN | 0.031944 | NaN | NaN | 0.053240 | NaN | NaN | ||||
Note here that there are blocks of non-zero terms with M=+/-1, these should drop out later (?) by sums over symmetry and/or other 3j terms… TBC…
Lambda term redux¶
Use existing function and force/sub-select terms…
[29]:
# Code adapted from mfblmXprod()
eulerAngs = np.array([0,0,0], ndmin=2)
# RX = ep.setPolGeoms(eulerAngs = eulerAngs) # This throws error in geomCalc.MFproj???? Something to do with form of terms passed to wD, line 970 vs. 976 in geomCalc.py
RX = ep.setPolGeoms() # (0,0,0) term in geomCalc.MFproj OK.
lambdaTerm, lambdaTable, lambdaD, QNsLambda = geomCalc.MFproj(RX = RX, form = 'xarray', phaseConvention = phaseConvention)
# lambdaTermResort = lambdaTerm.squeeze().drop('l').drop('lp') # This removes photon (l,lp) dims fully.
lambdaTermResort = lambdaTerm.squeeze(['l','lp']).drop(['l','lp']).sel({'Labels':'z'}) # Safe squeeze & drop of selected singleton dims only.
[30]:
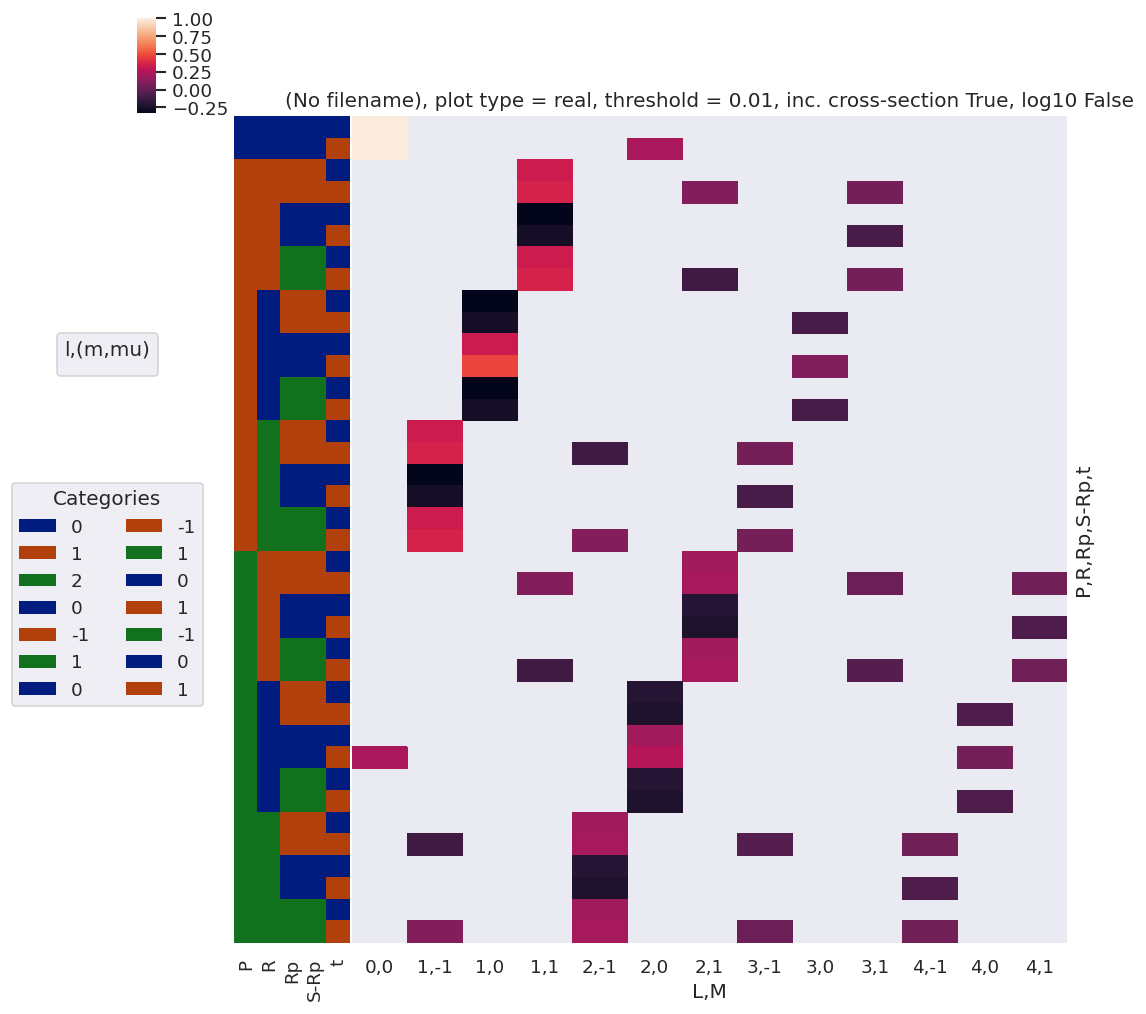
# Plot
xDim = {'PRp':['P','Rp']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(lambdaTermResort, xDim=xDim, pType = 'r')
daPlotpd
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[30]:
| P | 0 | 1 | 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Rp | 0 | -1 | 0 | 1 | -2 | -1 | 0 | 1 | 2 | ||
| R | mu | mup | |||||||||
| -2 | 1 | 1 | NaN | NaN | NaN | NaN | 0.447214 | NaN | NaN | NaN | NaN |
| -1 | 0 | 1 | NaN | -0.408248 | NaN | NaN | NaN | 0.316228 | NaN | NaN | NaN |
| 1 | 0 | NaN | 0.408248 | NaN | NaN | NaN | 0.316228 | NaN | NaN | NaN | |
| 0 | -1 | 1 | 0.57735 | NaN | -0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN |
| 0 | 0 | -0.57735 | NaN | NaN | NaN | NaN | NaN | 0.365148 | NaN | NaN | |
| 1 | -1 | 0.57735 | NaN | 0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN | |
| 1 | -1 | 0 | NaN | NaN | NaN | -0.408248 | NaN | NaN | NaN | 0.316228 | NaN |
| 0 | -1 | NaN | NaN | NaN | 0.408248 | NaN | NaN | NaN | 0.316228 | NaN | |
| 2 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.447214 |
Check component terms are as expected¶
Should have R = Rp for z case, and wD terms = 1 or 0.
[31]:
lambdaTablepd, _ = ep.util.multiDimXrToPD(lambdaTable, colDims=xDim, dropna=True)
lambdaTablepd
[31]:
| P | 0 | 1 | 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rp | 0 | -1 | 0 | 1 | -2 | -1 | 0 | 1 | 2 | ||||
| R | l | lp | mu | mup | |||||||||
| -2 | 1 | 1 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.447214 |
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.316228 | NaN | ||||
| 1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.182574 | NaN | NaN | ||||
| 0 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.316228 | NaN | |||
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.365148 | NaN | NaN | ||||
| 1 | NaN | NaN | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.182574 | NaN | NaN | |||
| 0 | NaN | NaN | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | NaN | NaN | NaN | NaN | 0.447214 | NaN | NaN | NaN | NaN | ||||
| -1 | 1 | 1 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.447214 |
| 0 | NaN | NaN | NaN | 0.408248 | NaN | NaN | NaN | -0.316228 | NaN | ||||
| 1 | NaN | NaN | -0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN | ||||
| 0 | -1 | NaN | NaN | NaN | -0.408248 | NaN | NaN | NaN | -0.316228 | NaN | |||
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.365148 | NaN | NaN | ||||
| 1 | NaN | 0.408248 | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | -1 | NaN | NaN | 0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN | |||
| 0 | NaN | -0.408248 | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | NaN | NaN | NaN | NaN | 0.447214 | NaN | NaN | NaN | NaN | ||||
| 0 | 1 | 1 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.447214 |
| 0 | NaN | NaN | NaN | 0.408248 | NaN | NaN | NaN | -0.316228 | NaN | ||||
| 1 | 0.57735 | NaN | -0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN | ||||
| 0 | -1 | NaN | NaN | NaN | -0.408248 | NaN | NaN | NaN | -0.316228 | NaN | |||
| 0 | -0.57735 | NaN | NaN | NaN | NaN | NaN | 0.365148 | NaN | NaN | ||||
| 1 | NaN | 0.408248 | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | -1 | 0.57735 | NaN | 0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN | |||
| 0 | NaN | -0.408248 | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | NaN | NaN | NaN | NaN | 0.447214 | NaN | NaN | NaN | NaN | ||||
| 1 | 1 | 1 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.447214 |
| 0 | NaN | NaN | NaN | 0.408248 | NaN | NaN | NaN | -0.316228 | NaN | ||||
| 1 | NaN | NaN | -0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN | ||||
| 0 | -1 | NaN | NaN | NaN | -0.408248 | NaN | NaN | NaN | -0.316228 | NaN | |||
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.365148 | NaN | NaN | ||||
| 1 | NaN | 0.408248 | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | -1 | NaN | NaN | 0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN | |||
| 0 | NaN | -0.408248 | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | NaN | NaN | NaN | NaN | 0.447214 | NaN | NaN | NaN | NaN | ||||
| 2 | 1 | 1 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.447214 |
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.316228 | NaN | ||||
| 1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.182574 | NaN | NaN | ||||
| 0 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.316228 | NaN | |||
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.365148 | NaN | NaN | ||||
| 1 | NaN | NaN | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.182574 | NaN | NaN | |||
| 0 | NaN | NaN | NaN | NaN | NaN | -0.316228 | NaN | NaN | NaN | ||||
| 1 | NaN | NaN | NaN | NaN | 0.447214 | NaN | NaN | NaN | NaN | ||||
[32]:
lambdaTermResortpd, _ = ep.util.multiDimXrToPD(lambdaTermResort, colDims=xDim, dropna=True)
lambdaTermResortpd
# Think this is as per lambdaTable terms, just different ordering - because lambdaTable doesn't include some phase switches?
[32]:
| P | 0 | 1 | 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Rp | 0 | -1 | 0 | 1 | -2 | -1 | 0 | 1 | 2 | ||
| R | mu | mup | |||||||||
| -2 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j |
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | ||
| 1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | ||
| 0 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | |
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | ||
| 1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | |
| 0 | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | 0.447214+0.000000j | NaN | NaN | NaN | NaN | ||
| -1 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j |
| 0 | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | ||
| 1 | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | ||
| 0 | -1 | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | |
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | ||
| 1 | NaN | -0.408248+0.000000j | NaN | NaN | NaN | 0.316228+0.000000j | NaN | NaN | NaN | ||
| 1 | -1 | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | |
| 0 | NaN | 0.408248+0.000000j | NaN | NaN | NaN | 0.316228+0.000000j | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | NaN | ||
| 0 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j |
| 0 | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | ||
| 1 | 0.577350+0.000000j | NaN | -0.408248+0.000000j | NaN | NaN | NaN | 0.182574+0.000000j | NaN | NaN | ||
| 0 | -1 | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | |
| 0 | -0.577350+0.000000j | NaN | NaN | NaN | NaN | NaN | 0.365148+0.000000j | NaN | NaN | ||
| 1 | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | ||
| 1 | -1 | 0.577350+0.000000j | NaN | 0.408248+0.000000j | NaN | NaN | NaN | 0.182574+0.000000j | NaN | NaN | |
| 0 | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | NaN | ||
| 1 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j |
| 0 | NaN | NaN | NaN | -0.408248+0.000000j | NaN | NaN | NaN | 0.316228+0.000000j | NaN | ||
| 1 | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | ||
| 0 | -1 | NaN | NaN | NaN | 0.408248+0.000000j | NaN | NaN | NaN | 0.316228+0.000000j | NaN | |
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | ||
| 1 | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | ||
| 1 | -1 | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | |
| 0 | NaN | 0.000000+0.000000j | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | NaN | ||
| 2 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.447214+0.000000j |
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | ||
| 1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | ||
| 0 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | |
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | ||
| 1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | |
| 0 | NaN | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | ||
| 1 | NaN | NaN | NaN | NaN | 0.000000+0.000000j | NaN | NaN | NaN | NaN | ||
[33]:
# wigner D term looks good.
lambdaDpd, _ = ep.util.multiDimXrToPD(lambdaD.sel({'Labels':'z'}), colDims=xDim, dropna=True)
lambdaDpd
[33]:
| P | 0 | 1 | 2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rp | 2 | 1 | 0 | -1 | -2 | 2 | 1 | 0 | -1 | -2 | 2 | 1 | 0 | -1 | -2 |
| R | |||||||||||||||
| 2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 1.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j |
| 1 | NaN | NaN | NaN | NaN | NaN | 0.000000-0.000000j | 1.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 1.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j |
| 0 | 0.000000-0.000000j | 0.000000-0.000000j | 1.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 1.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 1.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j |
| -1 | NaN | NaN | NaN | NaN | NaN | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 1.000000+0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 1.000000+0.000000j | 0.000000-0.000000j |
| -2 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 0.000000-0.000000j | 1.000000+0.000000j |
[34]:
# NOTE - accidental correlation R==Rp here unless dim is dropped
# xDim = {'PRp':['P','Rp']}
# lambdaDpd, _ = ep.util.multiDimXrToPD(lambdaD.sel({'Labels':'z'}).unstack().sum('R'), colDims=xDim, dropna=True, squeeze=False) # Throwing output errors... not sure why, has values and dims when tested at cmd???
# lambdaDpd
[35]:
# NOTE - accidental correlation R==Rp here unless dim is dropped
xDim = {'PRp':['P','Rp']}
lambdaTermResortpd, _ = ep.util.multiDimXrToPD(lambdaTermResort.sum('R'), colDims=xDim, dropna=True)
lambdaTermResortpd
[35]:
| P | 0 | 1 | 2 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rp | -2 | -1 | 0 | 1 | 2 | -2 | -1 | 0 | 1 | 2 | -2 | -1 | 0 | 1 | 2 | |
| mu | mup | |||||||||||||||
| -1 | -1 | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.447214+0.000000j |
| 0 | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | -0.408248+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.316228+0.000000j | 0.000000+0.000000j | |
| 1 | 0.000000+0.000000j | 0.000000+0.000000j | 0.577350+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | -0.408248+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.182574+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | |
| 0 | -1 | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.408248+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.316228+0.000000j | 0.000000+0.000000j |
| 0 | 0.000000+0.000000j | 0.000000+0.000000j | -0.577350+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.365148+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | |
| 1 | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | -0.408248+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.316228+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | |
| 1 | -1 | 0.000000+0.000000j | 0.000000+0.000000j | 0.577350+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.408248+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.182574+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j |
| 0 | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.408248+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.316228+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | |
| 1 | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.447214+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | 0.000000+0.000000j | |
Build full calculation from functions¶
Use mfblmGeom.py as template: basically just need modified lambda term as above, and new alignment term, and rest of calculation should be identical.
[36]:
# Check polProd term - incorporate alignment term here...?
# Existing terms
# polProd = (EPRXresort * lambdaTermResort)
# sumDimsPol = ['P','R','Rp','p']
# polProd = polProd.sum(sumDimsPol)
# Test with alignment term
polProd = (EPRXresort * lambdaTermResort * AFterm)
sumDimsPol = ['P','R','Rp','p', 'S-Rp']
polProd = polProd.sum(sumDimsPol)
# Looks OK - keeps correct dims in test case! 270 terms.
NOW implemented in ep.geomFunc.afblmGeom.py
Testing…¶
16/06/20
Test code adapted from previous round of AF tests, http://localhost:8888/lab/tree/dev/ePSproc/ePSproc_AFBLM_calcs_bench_100220.ipynb
See also MFBLM test code, http://localhost:8888/lab/tree/dev/ePSproc/geometric_method_dev_2020/geometric_method_dev_pt2_170320_v090620.ipynb
Load data¶
[37]:
# Load data from modPath\data
dataPath = os.path.join(modPath, 'data', 'photoionization')
dataFile = os.path.join(dataPath, 'n2_3sg_0.1-50.1eV_A2.inp.out') # Set for sample N2 data for testing
# Scan data file
dataSet = ep.readMatEle(fileIn = dataFile)
dataXS = ep.readMatEle(fileIn = dataFile, recordType = 'CrossSection') # XS info currently not set in NO2 sample file.
*** ePSproc readMatEle(): scanning files for DumpIdy segments.
*** Scanning file(s)
['D:\\code\\github\\ePSproc\\data\\photoionization\\n2_3sg_0.1-50.1eV_A2.inp.out']
*** Reading ePS output file: D:\code\github\ePSproc\data\photoionization\n2_3sg_0.1-50.1eV_A2.inp.out
Expecting 51 energy points.
Expecting 2 symmetries.
Scanning CrossSection segments.
Expecting 102 DumpIdy segments.
Found 102 dumpIdy segments (sets of matrix elements).
Processing segments to Xarrays...
Processed 102 sets of DumpIdy file segments, (0 blank)
*** ePSproc readMatEle(): scanning files for CrossSection segments.
*** Scanning file(s)
['D:\\code\\github\\ePSproc\\data\\photoionization\\n2_3sg_0.1-50.1eV_A2.inp.out']
*** Reading ePS output file: D:\code\github\ePSproc\data\photoionization\n2_3sg_0.1-50.1eV_A2.inp.out
Expecting 51 energy points.
Expecting 2 symmetries.
Scanning CrossSection segments.
Expecting 3 CrossSection segments.
Found 3 CrossSection segments (sets of results).
Processed 3 sets of CrossSection file segments, (0 blank)
Plot ePS results (isotropic case)¶
[38]:
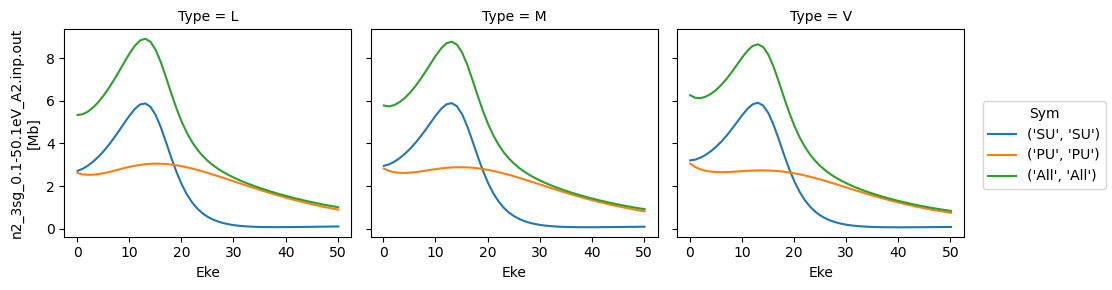
# Plot cross sections using Xarray functionality
# Set here to plot per file - should add some logic to combine files.
for data in dataXS:
daPlot = data.sel(XC='SIGMA')
daPlot.plot.line(x='Eke', col='Type')
[38]:
<xarray.plot.facetgrid.FacetGrid at 0x1da1a0574e0>
[39]:
# Repeat for betas
for data in dataXS:
daPlot = data.sel(XC='BETA')
daPlot.plot.line(x='Eke', col='Type')
[39]:
<xarray.plot.facetgrid.FacetGrid at 0x1da1838cdd8>
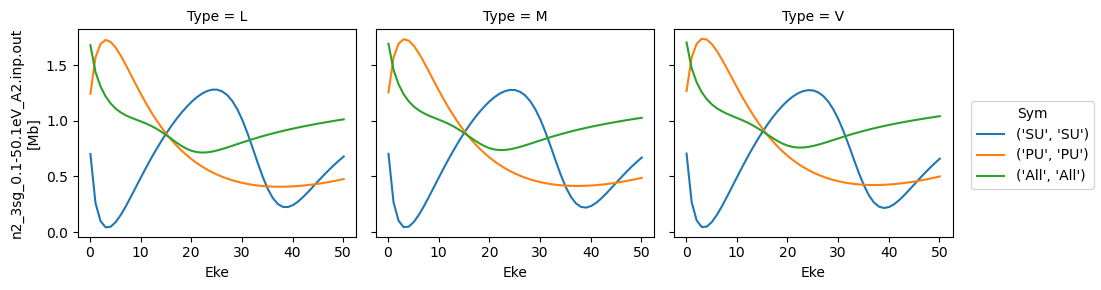
Try new AF calculation - isotropic (default) case¶
[40]:
# Tabulate & plot matrix elements vs. Eke
selDims = {'it':1, 'Type':'L'}
# selDims = {'Type':'L'}
matE = dataSet[0].sel(selDims) # Set for N2 case, length-gauge results only.
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(matE, xDim = 'Eke', pType = 'r', fillna = True)
daPlotpd
Plotting data n2_3sg_0.1-50.1eV_A2.inp.out, pType=r, thres=0.01, with Seaborn
[40]:
| Eke | 0.1 | 1.1 | 2.1 | 3.1 | 4.1 | 5.1 | 6.1 | 7.1 | 8.1 | 9.1 | ... | 41.1 | 42.1 | 43.1 | 44.1 | 45.1 | 46.1 | 47.1 | 48.1 | 49.1 | 50.1 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cont | Targ | Total | l | m | mu | |||||||||||||||||||||
| PU | SG | PU | 1 | -1 | 1 | -6.203556 | 7.496908 | 3.926892 | 1.071093 | -0.335132 | -1.043391 | -1.396885 | -1.554984 | -1.598812 | -1.573327 | ... | -0.396306 | -0.422225 | -0.448003 | -0.473466 | -0.498463 | -0.522867 | -0.546573 | -0.569493 | -0.591558 | -0.612712 |
| 1 | -1 | -6.203556 | 7.496908 | 3.926892 | 1.071093 | -0.335132 | -1.043391 | -1.396885 | -1.554984 | -1.598812 | -1.573327 | ... | -0.396306 | -0.422225 | -0.448003 | -0.473466 | -0.498463 | -0.522867 | -0.546573 | -0.569493 | -0.591558 | -0.612712 | ||||
| 3 | -1 | 1 | -2.090641 | -1.723467 | -3.571018 | -1.703191 | 0.232612 | 1.862713 | 3.201022 | 4.298839 | 5.198215 | 5.929303 | ... | 1.200463 | 1.040074 | 0.892501 | 0.757189 | 0.633556 | 0.521004 | 0.418928 | 0.326726 | 0.243800 | 0.169566 | |||
| 1 | -1 | -2.090641 | -1.723467 | -3.571018 | -1.703191 | 0.232612 | 1.862713 | 3.201022 | 4.298839 | 5.198215 | 5.929303 | ... | 1.200463 | 1.040074 | 0.892501 | 0.757189 | 0.633556 | 0.521004 | 0.418928 | 0.326726 | 0.243800 | 0.169566 | ||||
| 5 | -1 | 1 | 0.000000 | 0.013246 | 0.000000 | -0.013096 | -0.024367 | -0.033455 | -0.042762 | -0.053765 | -0.067354 | -0.083946 | ... | -0.325544 | -0.318791 | -0.312332 | -0.306211 | -0.300456 | -0.295091 | -0.290130 | -0.285584 | -0.281453 | -0.277737 | |||
| 1 | -1 | 0.000000 | 0.013246 | 0.000000 | -0.013096 | -0.024367 | -0.033455 | -0.042762 | -0.053765 | -0.067354 | -0.083946 | ... | -0.325544 | -0.318791 | -0.312332 | -0.306211 | -0.300456 | -0.295091 | -0.290130 | -0.285584 | -0.281453 | -0.277737 | ||||
| 7 | -1 | 1 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.027469 | 0.028083 | 0.028678 | 0.029257 | 0.029823 | 0.030377 | 0.030923 | 0.031461 | 0.031994 | 0.032523 | |||
| 1 | -1 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.027469 | 0.028083 | 0.028678 | 0.029257 | 0.029823 | 0.030377 | 0.030923 | 0.031461 | 0.031994 | 0.032523 | ||||
| SU | SG | SU | 1 | 0 | 0 | 6.246520 | -10.081763 | -8.912214 | -5.342049 | -3.160539 | -1.795783 | -0.867993 | -0.174154 | 0.400643 | 0.926420 | ... | -0.854886 | -0.940017 | -1.021577 | -1.099776 | -1.174787 | -1.246759 | -1.315814 | -1.382058 | -1.445582 | -1.506467 |
| 3 | 0 | 0 | 2.605768 | 2.775108 | 4.733473 | 1.677812 | -1.450830 | -4.187395 | -6.554491 | -8.601759 | -10.343109 | -11.747922 | ... | -0.293053 | -0.441416 | -0.579578 | -0.708075 | -0.827415 | -0.938075 | -1.040506 | -1.135134 | -1.222361 | -1.302566 | |||
| 5 | 0 | 0 | 0.000000 | -0.020864 | 0.000000 | 0.024263 | 0.042694 | 0.059142 | 0.077308 | 0.099330 | 0.126227 | 0.157745 | ... | 0.490499 | 0.511546 | 0.531810 | 0.551281 | 0.569951 | 0.587815 | 0.604868 | 0.621107 | 0.636528 | 0.651132 | |||
| 7 | 0 | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | -0.039566 | -0.041422 | -0.043265 | -0.045092 | -0.046901 | -0.048689 | -0.050453 | -0.052190 | -0.053899 | -0.055577 |
12 rows × 51 columns
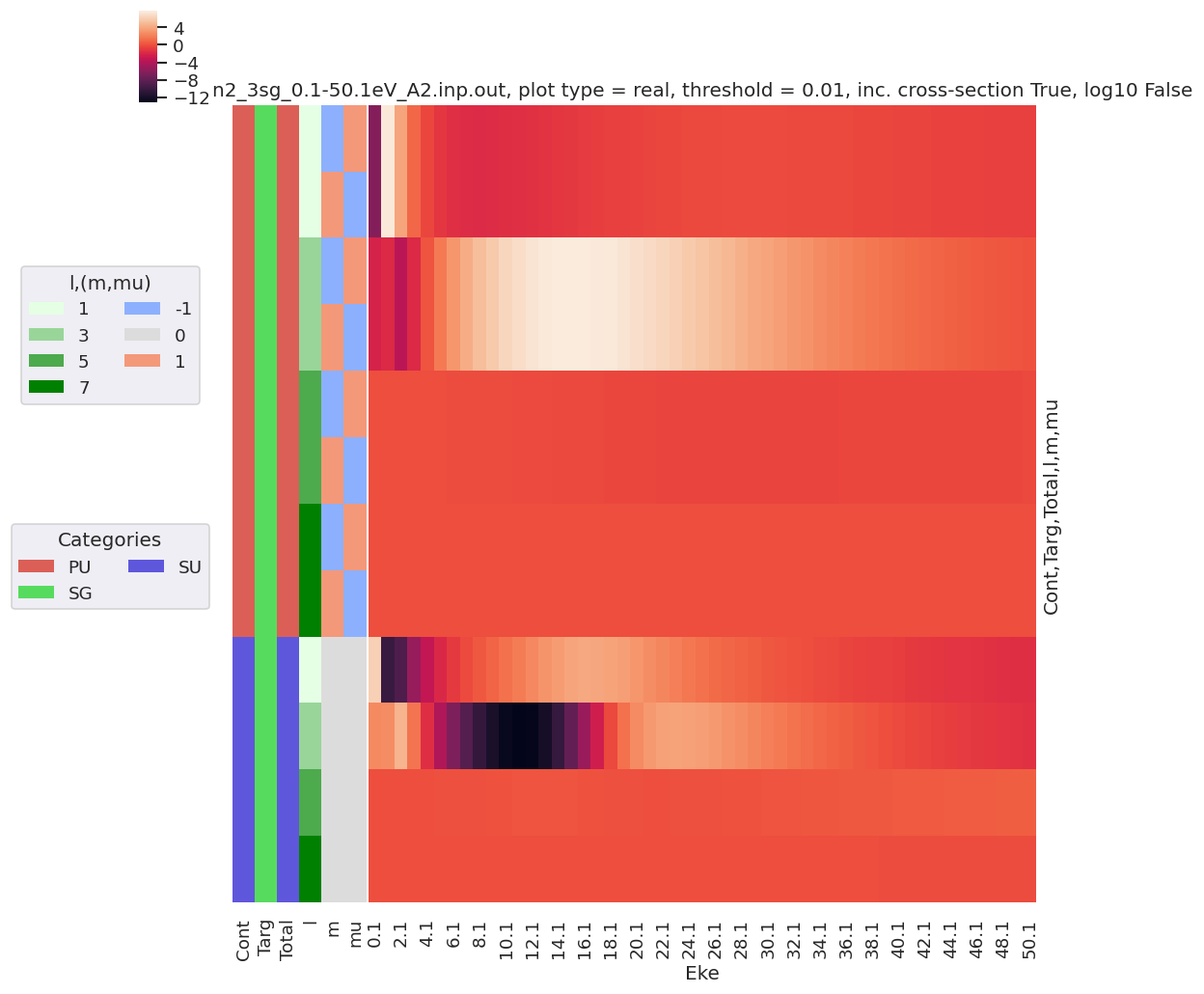
Check BetaTerm - QN switch¶
[41]:
# Set parameters
SFflag = False
phaseConvention = 'E'
thres = 1e-1
selDims = {'it':1, 'Type':'L'}
thresDims = 'Eke'
# sumDims = ['mu', 'mup', 'l','lp','m','mp','S-Rp']
sumDims = ['mu', 'mup', 'l','lp','m','mp']
sumDimsPol = ['P','R','Rp','p']
# Set matrix elements
matE = dataSet[0].copy()
# Setting this here gives usual problem (non-matching XS values to getCro)
# Now testing multiplication at end of calc...
# if SFflag:
# matE.values = matE * matE.SF
matEthres = ep.matEleSelector(matE, thres = thres, inds = selDims, dims = thresDims, sq = True, drop = True)
# Code as per afblmGeom.py for testing - phase issues somewhere here...
QNs = ep.geomFunc.genllpMatE(matEthres, phaseConvention = phaseConvention)
QNsBLMtable = QNs.copy()
phaseCons = ep.geomFunc.setPhaseConventions(phaseConvention = phaseConvention)
# Switch signs (m,M) before 3j calcs.
# if phaseCons['mfblmCons']['BLMmPhase']:
# QNsBLMtable[:,3] *= -1
# QNsBLMtable[:,5] *= -1
#**** TESTING
# QNsBLMtable[:,3] *= -1 # m > -m # IF set, get S-Rp = -2....+2, otherwise only -1....+1
# QNsBLMtable[:,5] *= -1
BLMtable = geomCalc.betaTerm(QNs = QNsBLMtable, form = 'xdaLM', phaseConvention = phaseConvention)
# if BLMtableResort is None:
# Apply additional phase convention
BLMtableResort = BLMtable.copy().unstack()
# if phaseCons['mfblmCons']['negMcoordSwap']:
# BLMtableResort['M'] *= -1
# if phaseCons['mfblmCons']['Mphase']:
# BLMtableResort *= np.power(-1, np.abs(BLMtableResort.M)) # Associated phase term
# if phaseCons['mfblmCons']['negmCoordSwap']:
# BLMtableResort['m'] *= -1 # 25/06/20 Currently sends M>0 terms to 0. But suspicious this is incorrect at matE selection...
# Full phase cons testing....
if phaseCons['mfblmCons']['negMcoordSwap']:
BLMtableResort['M'] *= -1
if phaseCons['mfblmCons']['Mphase']:
BLMtableResort *= np.power(-1, np.abs(BLMtableResort.M)) # Associated phase term
if phaseCons['mfblmCons']['negmCoordSwap']:
BLMtableResort['m'] *= -1
if phaseCons['mfblmCons']['mPhase']:
BLMtableResort *= np.power(-1, np.abs(BLMtableResort.m)) # Associated phase term
# RENAME, M > (S-R') for AF case - this correctly allows for all MF projections!!!
# Some MF phase cons as applied above may also be incorrect?
BLMtableResort = BLMtableResort.rename({'M':'S-Rp'})
# BLMtableResort['m'] *= -1
[42]:
# Plot
xDim = {'LSRp':['L','S-Rp']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(BLMtableResort, xDim=xDim, pType = 'r')
# pd.options.display.max_rows = 50
pd.set_option('display.max_rows', 50)
daPlotpd[0:20]
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
[42]:
| L | 0 | 2 | 4 | ... | 8 | 10 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-Rp | 0 | -2 | -1 | 0 | 1 | 2 | -2 | -1 | 0 | 1 | ... | -2 | -1 | 0 | 1 | 2 | -2 | -1 | 0 | 1 | 2 | |||
| l | lp | m | mp | |||||||||||||||||||||
| 1 | 1 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | -0.309019 | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 0 | NaN | NaN | NaN | NaN | 0.218510 | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | 0.282095 | NaN | NaN | -0.126157 | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 0 | -1 | NaN | NaN | NaN | NaN | -0.218510 | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 0 | 0.282095 | NaN | NaN | 0.252313 | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | NaN | NaN | -0.218510 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | -1 | 0.282095 | NaN | NaN | -0.126157 | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 0 | NaN | NaN | 0.218510 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | NaN | -0.309019 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 3 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | 0.082589 | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 0 | NaN | NaN | NaN | NaN | -0.143048 | NaN | NaN | NaN | NaN | 0.194664 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | NaN | NaN | NaN | 0.202301 | NaN | NaN | NaN | NaN | -0.150786 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 0 | -1 | NaN | NaN | NaN | NaN | -0.233597 | NaN | NaN | NaN | NaN | -0.238414 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 0 | NaN | NaN | NaN | 0.247767 | NaN | NaN | NaN | NaN | 0.246233 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | NaN | NaN | -0.233597 | NaN | NaN | NaN | NaN | -0.238414 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | -1 | NaN | NaN | NaN | 0.202301 | NaN | NaN | NaN | NaN | -0.150786 | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||
| 0 | NaN | NaN | -0.143048 | NaN | NaN | NaN | NaN | 0.194664 | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | NaN | 0.082589 | NaN | NaN | NaN | NaN | -0.238414 | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 5 | -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.155288 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
20 rows × 26 columns
[43]:
# EPR
EPRX = geomCalc.EPR(form = 'xarray', p = p).unstack().sel({'R-p':0}).drop('R-p')
EPRXresort = EPRX.squeeze(['l','lp']).drop(['l','lp']) # Safe squeeze & drop of selected singleton dims only.
if phaseCons['mfblmCons']['negRcoordSwap']:
EPRXresort['R'] *= -1
# Lambda
RX = ep.setPolGeoms()
# *** Lambda term
lambdaTerm, lambdaTable, lambdaD, _ = geomCalc.MFproj(RX = RX, form = 'xarray', phaseConvention = phaseConvention)
# lambdaTermResort = lambdaTerm.squeeze().drop('l').drop('lp') # This removes photon (l,lp) dims fully.
# lambdaTermResort = lambdaTerm.squeeze(['l','lp']).drop(['l','lp']) # Safe squeeze & drop of selected singleton dims only.
lambdaTermResort = lambdaTerm.squeeze(['l','lp']).drop(['l','lp']).sel({'Labels':'z'}).sum('R') # Safe squeeze & drop of selected singleton dims only, select (0,0,0) term only for pol. geometry.
# AF term
AKQS = ep.setADMs() # If not passed, set to defaults - A(0,0,0)=1 term only, i.e. isotropic distribution.
AFterm, DeltaKQS = geomCalc.deltaLMKQS(EPRXresort, AKQS, phaseConvention = phaseConvention)
[44]:
EPRX.unstack().coords
[44]:
Coordinates:
* l (l) int64 1
* lp (lp) int64 1
* P (P) int64 0 1 2
* p (p) int64 0
* R (R) int64 -1 0 1
[45]:
lambdaTerm.dims
[45]:
('Rp', 'l', 'lp', 'P', 'mu', 'mup', 'R', 'Labels')
[46]:
lambdaTermResort.dims
[46]:
('Rp', 'P', 'mu', 'mup')
[47]:
EPRX.squeeze()
[47]:
<xarray.DataArray (P: 3, R: 3)>
array([[ nan, -0.57735027, nan],
[ nan, nan, nan],
[ nan, 0.81649658, nan]])
Coordinates:
l int64 1
lp int64 1
* P (P) int64 0 1 2
p int64 0
* R (R) int64 -1 0 1
Attributes:
dataType: EPR
phaseCons: {'phaseConvention': 'S', 'genMatEcons': {'negm': False}, 'EPR...[48]:
plotDimsRed = ['l', 'p', 'lp']
xDim = {'PR':['P','R']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(EPRXresort, plotDims=plotDimsRed, xDim=xDim, pType = 'r', squeeze = False)
daPlotpd
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[48]:
| P | 0 | 2 |
|---|---|---|
| R | 0 | 0 |
| p | ||
| 0 | -0.57735 | 0.816497 |
[49]:
# plotDimsRed = ['l', 'm', 'lp', 'mp']
xDim = {'LSRp':['P','Rp']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
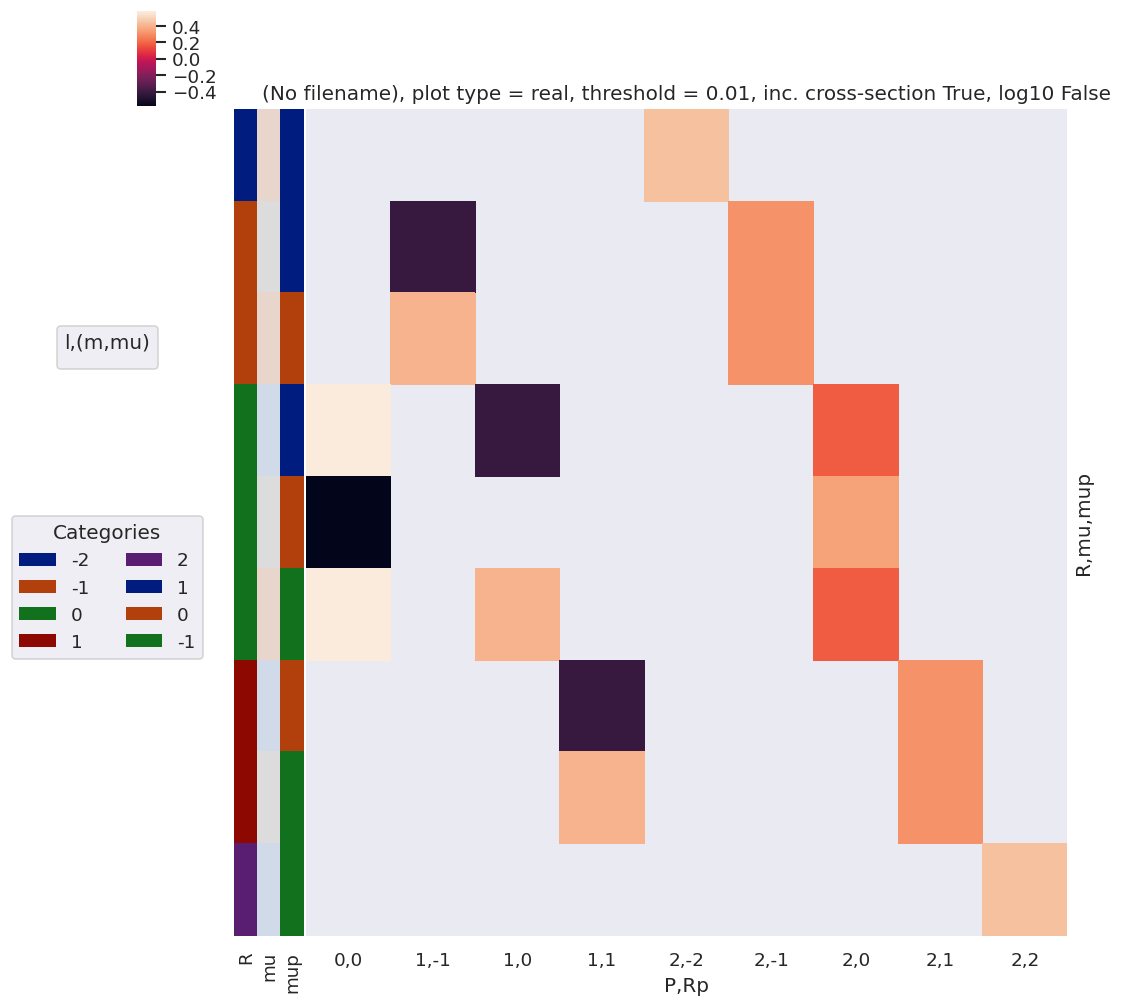
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(lambdaTerm.sel({'Labels':'z'}), xDim=xDim, pType = 'r', squeeze = False)
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(lambdaTermResort, xDim=xDim, pType = 'r', squeeze = False)
daPlotpd[0:20]
Set dataType (No dataType)
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[49]:
| P | 0 | 1 | 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rp | 0 | -1 | 0 | 1 | -2 | -1 | 0 | 1 | 2 | |
| mu | mup | |||||||||
| -1 | -1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.447214 |
| 0 | NaN | NaN | NaN | -0.408248 | NaN | NaN | NaN | 0.316228 | NaN | |
| 1 | 0.57735 | NaN | -0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN | |
| 0 | -1 | NaN | NaN | NaN | 0.408248 | NaN | NaN | NaN | 0.316228 | NaN |
| 0 | -0.57735 | NaN | NaN | NaN | NaN | NaN | 0.365148 | NaN | NaN | |
| 1 | NaN | -0.408248 | NaN | NaN | NaN | 0.316228 | NaN | NaN | NaN | |
| 1 | -1 | 0.57735 | NaN | 0.408248 | NaN | NaN | NaN | 0.182574 | NaN | NaN |
| 0 | NaN | 0.408248 | NaN | NaN | NaN | 0.316228 | NaN | NaN | NaN | |
| 1 | NaN | NaN | NaN | NaN | 0.447214 | NaN | NaN | NaN | NaN | |
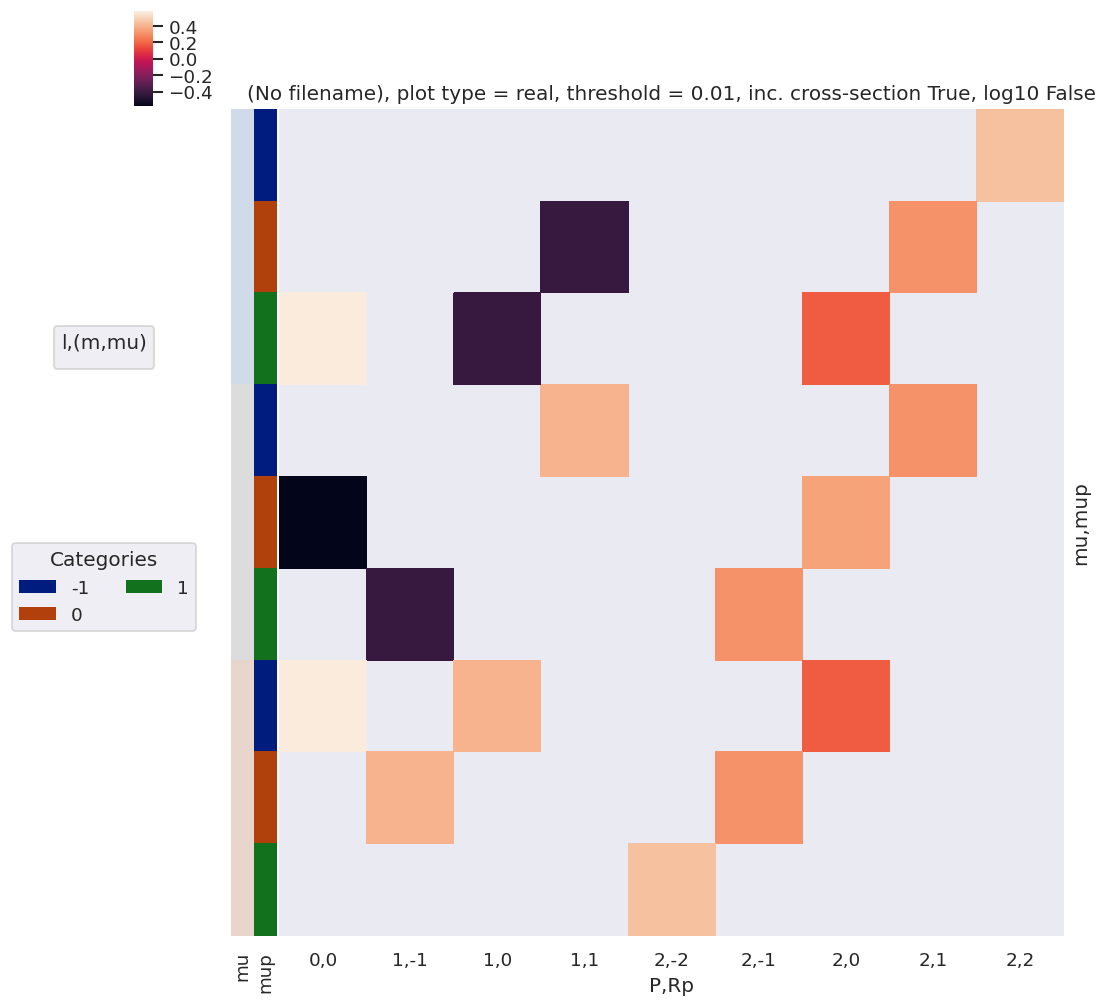
[50]:
# plotDimsRed = ['l', 'm', 'lp', 'mp']
xDim = {'LSRp':['L','S-Rp']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(DeltaKQS, xDim=xDim, pType = 'r')
daPlotpd
Set dataType (No dataType)
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\core\nputils.py:215: RuntimeWarning:
All-NaN slice encountered
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
[50]:
| L | 0 | 1 | 2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-Rp | 0 | -1 | 0 | 1 | -2 | -1 | 0 | 1 | 2 | ||||||
| K | M | P | Q | R | Rp | S | |||||||||
| 0 | -1 | 1 | 0 | 1 | -1 | 0 | NaN | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN |
| 0 | 0 | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | |||||
| 1 | 0 | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||||
| 2 | 0 | 1 | -2 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | ||
| -1 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | |||||
| 0 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | |||||
| 1 | 0 | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | NaN | NaN | |||||
| 2 | 0 | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | NaN | NaN | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |
| 1 | 0 | 0 | -1 | 0 | NaN | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | ||
| 0 | 0 | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | |||||
| 1 | 0 | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||||
| 2 | 0 | 0 | -2 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.2 | ||
| -1 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | NaN | |||||
| 0 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | NaN | |||||
| 1 | 0 | NaN | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | NaN | |||||
| 2 | 0 | NaN | NaN | NaN | NaN | 0.2 | NaN | NaN | NaN | NaN | |||||
| 1 | 1 | 0 | -1 | -1 | 0 | NaN | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | |
| 0 | 0 | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | |||||
| 1 | 0 | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||||
| 2 | 0 | -1 | -2 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | ||
| -1 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | |||||
| 0 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | |||||
| 1 | 0 | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | NaN | NaN | |||||
| 2 | 0 | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | NaN | NaN | |||||
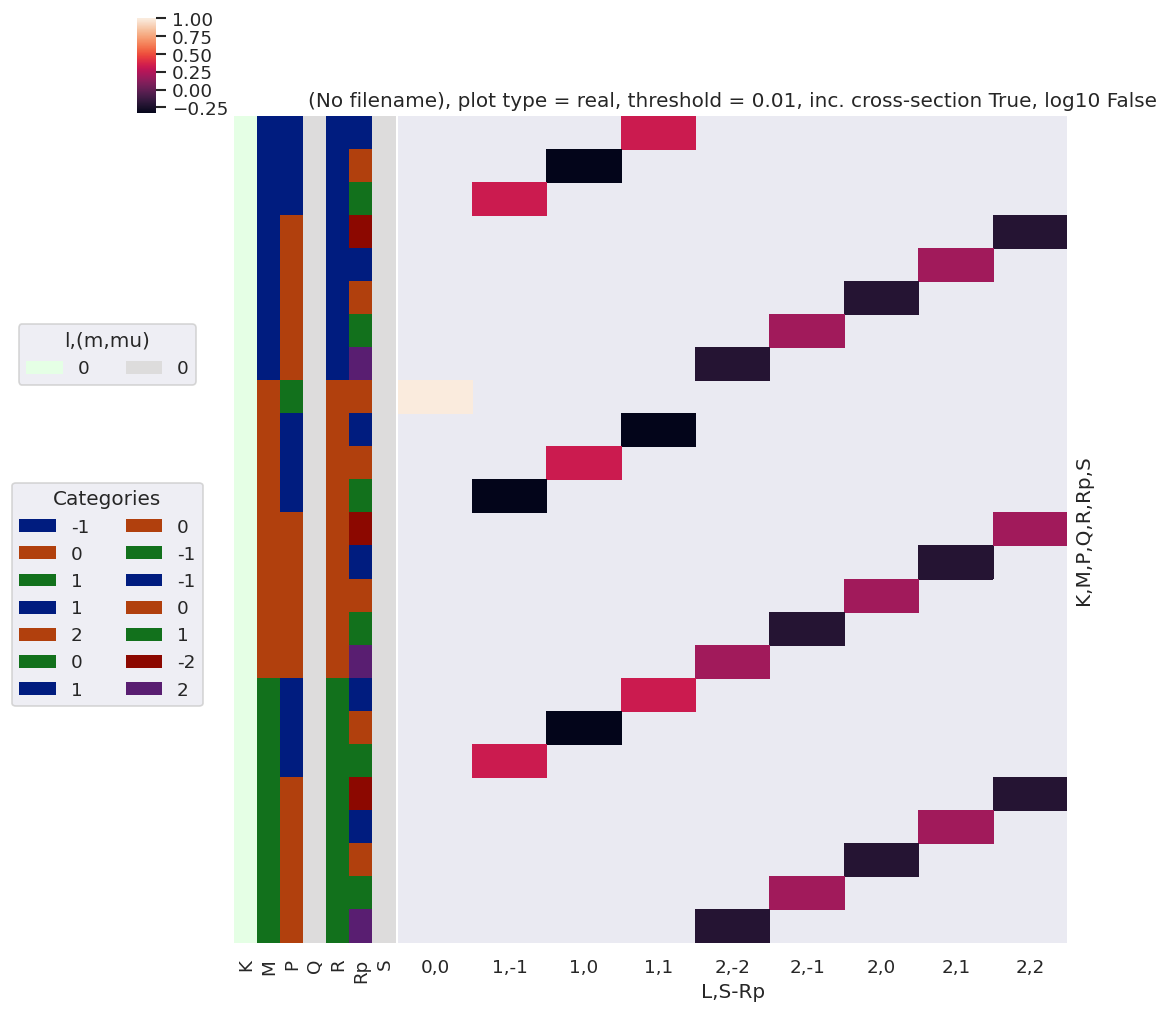
[51]:
# plotDimsRed = ['l', 'm', 'lp', 'mp']
xDim = {'LSRp':['L','S-Rp']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(AFterm, xDim=xDim, pType = 'r')
daPlotpd
Set dataType (No dataType)
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[51]:
| L | 0 | 1 | 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-Rp | 0 | -1 | 0 | 1 | -2 | -1 | 0 | 1 | 2 | ||||
| M | P | R | Rp | t | |||||||||
| -1 | 1 | 1 | -1 | 0 | NaN | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN |
| 0 | 0 | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | 0 | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 2 | 1 | -2 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | |
| -1 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | |||
| 0 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | |||
| 1 | 0 | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | NaN | NaN | |||
| 2 | 0 | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | NaN | NaN | |||
| 0 | 0 | 0 | 0 | 0 | 1.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 1 | 0 | -1 | 0 | NaN | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | |
| 0 | 0 | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | 0 | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 2 | 0 | -2 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.2 | |
| -1 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | NaN | |||
| 0 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | NaN | |||
| 1 | 0 | NaN | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | NaN | |||
| 2 | 0 | NaN | NaN | NaN | NaN | 0.2 | NaN | NaN | NaN | NaN | |||
| 1 | 1 | -1 | -1 | 0 | NaN | NaN | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN |
| 0 | 0 | NaN | NaN | -0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 1 | 0 | NaN | 0.333333 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||
| 2 | -1 | -2 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | |
| -1 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | |||
| 0 | 0 | NaN | NaN | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | |||
| 1 | 0 | NaN | NaN | NaN | NaN | NaN | 0.2 | NaN | NaN | NaN | |||
| 2 | 0 | NaN | NaN | NaN | NaN | -0.2 | NaN | NaN | NaN | NaN | |||
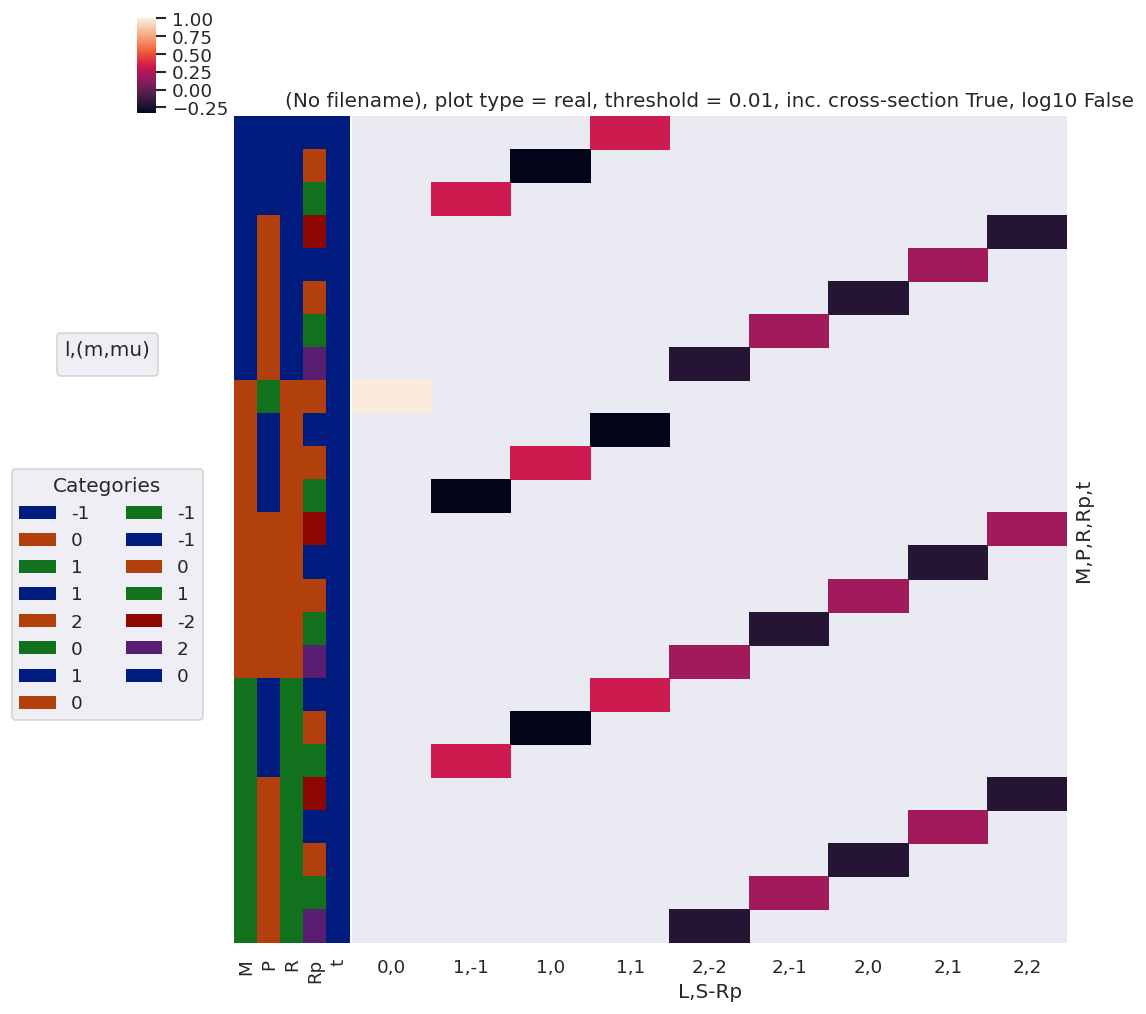
[52]:
#*** Products
# Matrix element pair-wise multiplication by (l,m,mu) dims
matEconj = matEthres.copy().conj()
# matEconj = matEconj.unstack().rename({'l':'lp','m':'mp','mu':'mup'}) # Full unstack
# matEmult = matEthres.unstack() * matEconj
matEconj = matEconj.unstack('LM').rename({'l':'lp','m':'mp','mu':'mup'}) # Unstack LM only.
matEmult = matEthres.unstack('LM') * matEconj
matEmult.attrs['dataType'] = 'multTest'
# Threshold product and drop dims.
# matEmult = ep.util.matEleSelector(matEmult, thres = thres, dims = thresDims)
matEmult = matEleSelector(matEmult, thres = thres, dims = thresDims)
# Apply additional phase conventions?
if phaseCons['afblmCons']['llpPhase']:
matEmult *= np.power(-1, np.abs(matEmult.l - matEmult.lp))
# matEmult['mp'] *= -1 # Quick test of mp phase
# Product terms with similar dims
BLMprod = matEmult * BLMtableResort # Unstacked case with phase correction - THIS DROPS SYM TERMS? Takes intersection of das - http://xarray.pydata.org/en/stable/computation.html#automatic-alignment
# polProd = (EPRXresort * lambdaTermResort).sum(sumDimsPol) # Sum polarization terms here to keep total dims minimal in product. Here dims = (mu,mup,Euler/Labels)
# polProd = (EPRXresort * lambdaTermResort) # Without polarization terms sum to allow for mupPhase below (reqs. p)
# Test with alignment term
# polProd = (EPRXresort * lambdaTermResort * AFterm)
# With additional phase change(s)
lTermTest = lambdaTermResort.copy()
AFtermTest = AFterm.copy()
# AFtermTest['Rp'] *= -1
# lTermTest['mup'] *=-1
polProd = (EPRXresort * lTermTest * AFtermTest)
# polProd = (lTermTest * AFtermTest) # 25/06/20 this multiplication seems to restrict S-Rp to -1...+1, not sure why. mu/mup phase? Rp phase? Neither (nor both) seems to fix the issue.
# Set additional phase term, (-1)^(mup-p) **** THIS MIGHT BE SPURIOUS FOR GENERAL EPR TENSOR CASE??? Not sure... but definitely won't work if p summed over above!
if phaseCons['mfblmCons']['mupPhase']:
mupPhaseTerm = np.power(-1, np.abs(polProd.mup - polProd.p))
polProd *= mupPhaseTerm
# Additional [P]^1/2 degen term, NOT included in EPR defn.
# Added 09/04/20
polProd *= np.sqrt(2*polProd.P+1)
[53]:
# Check terms...
# xDim = {'LM':['L','M']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(polProd, xDim=xDim, pType = 'r') #, thres=None)
daPlotpd
Set dataType (No dataType)
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\core\nputils.py:215: RuntimeWarning:
All-NaN slice encountered
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
[53]:
| L | 0 | 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-Rp | 0 | -2 | -1 | 0 | 1 | 2 | |||||||
| M | P | R | Rp | mu | mup | p | t | ||||||
| 0 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 0.333333 | NaN | NaN | NaN | NaN | NaN |
| 0 | 0 | 0 | 0 | 0.333333 | NaN | NaN | NaN | NaN | NaN | ||||
| 1 | -1 | 0 | 0 | 0.333333 | NaN | NaN | NaN | NaN | NaN | ||||
| 2 | 0 | -2 | 1 | 1 | 0 | 0 | NaN | NaN | NaN | NaN | NaN | -0.163299 | |
| -1 | 0 | 1 | 0 | 0 | NaN | NaN | NaN | NaN | 0.11547 | NaN | |||
| 1 | 0 | 0 | 0 | NaN | NaN | NaN | NaN | -0.11547 | NaN | ||||
| 0 | -1 | 1 | 0 | 0 | NaN | NaN | NaN | -0.066667 | NaN | NaN | |||
| 0 | 0 | 0 | 0 | NaN | NaN | NaN | 0.133333 | NaN | NaN | ||||
| 1 | -1 | 0 | 0 | NaN | NaN | NaN | -0.066667 | NaN | NaN | ||||
| 1 | -1 | 0 | 0 | 0 | NaN | NaN | -0.11547 | NaN | NaN | NaN | |||
| 0 | -1 | 0 | 0 | NaN | NaN | 0.11547 | NaN | NaN | NaN | ||||
| 2 | -1 | -1 | 0 | 0 | NaN | -0.163299 | NaN | NaN | NaN | NaN | |||
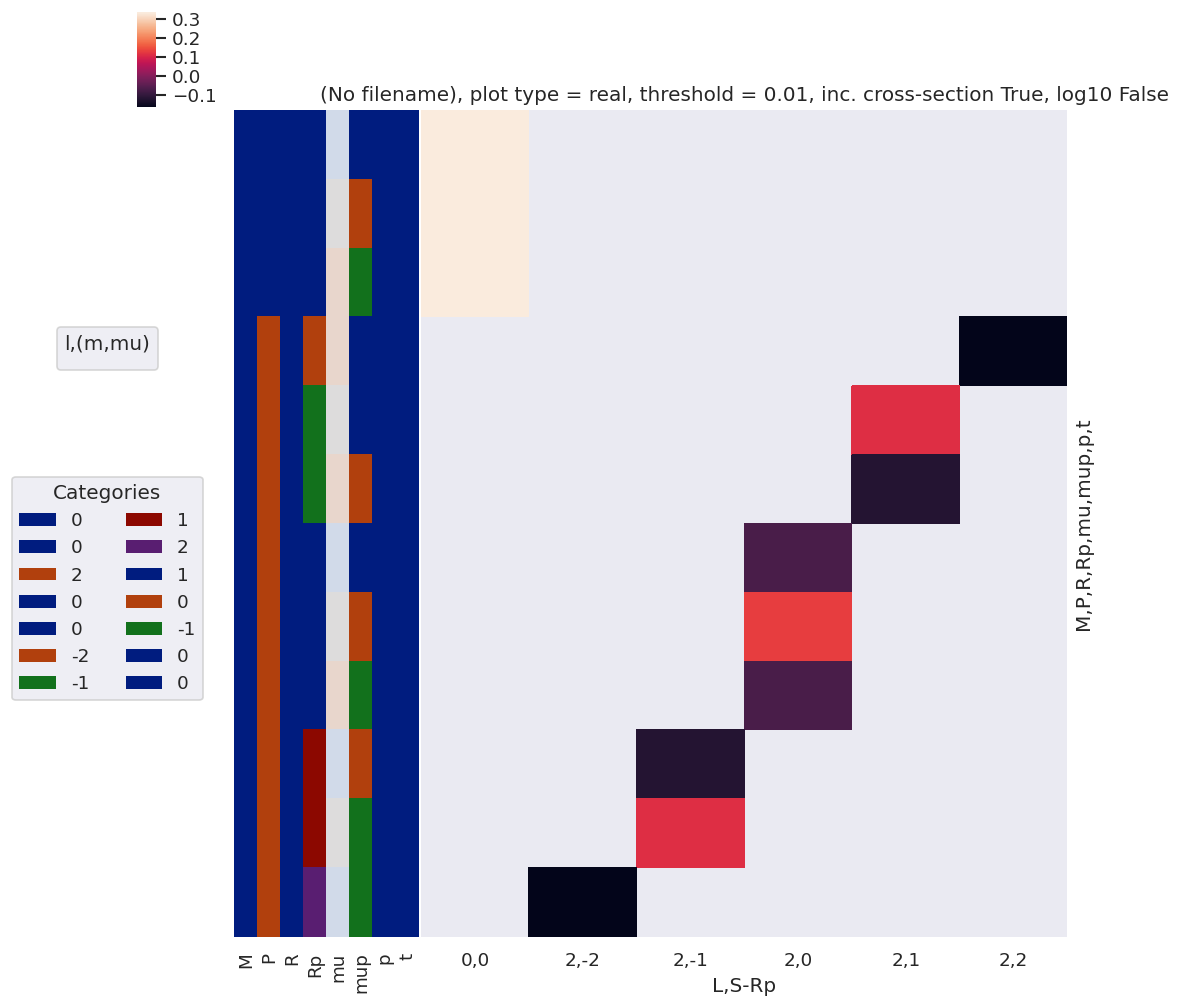
[54]:
polProd = polProd.sum(sumDimsPol)
# polProd = matEleSelector(polProd, thres = thres) # Select over dims for reduction.
# Test big mult...
# mTerm = polProd.sel({'R':0,'Labels':'z'}) * BLMprod.sum(['Total']) # With selection of z geom. # BLMprod.sum(['Cont', 'Targ', 'Total'])
# mTerm = polProd.sel({'R':0}) * BLMprod # BLMprod.sum(['Cont', 'Targ', 'Total'])
mTerm = polProd * BLMprod
[55]:
# Check terms... BLMprod
xDim = {'LSRp':['L','S-Rp']}
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(testMult, plotDims=plotDimsRed, xDim=xDim, pType = 'r')
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(BLMprod.sel({'Eke':0.1}), xDim=xDim, pType = 'r')
daPlotpd
Set dataType (No dataType)
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\core\nputils.py:215: RuntimeWarning:
All-NaN slice encountered
Plotting data (No filename), pType=r, thres=0.01, with Seaborn
[55]:
| L | 0 | 2 | 4 | 6 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-Rp | 0 | -2 | 0 | 2 | -2 | 0 | 2 | -2 | 0 | 2 | ||||||||
| Cont | Targ | Total | l | lp | m | mp | mu | mup | ||||||||||
| PU | SG | PU | 1 | 1 | -1 | -1 | 1 | 1 | NaN | NaN | NaN | -1.098886 | NaN | NaN | NaN | NaN | NaN | NaN |
| 1 | 1 | -1 | 1.003141 | NaN | -0.448618 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||||
| 1 | -1 | -1 | 1 | 1.003141 | NaN | -0.448618 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | |||||
| 1 | -1 | -1 | NaN | -1.098886 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ||||||
| 3 | -1 | -1 | 1 | 1 | NaN | NaN | NaN | 0.020515 | NaN | NaN | -0.059223 | NaN | NaN | NaN | ||||
| 1 | 1 | -1 | NaN | NaN | 0.050252 | NaN | NaN | -0.037456 | NaN | NaN | NaN | NaN | ||||||
| 1 | -1 | -1 | 1 | NaN | NaN | 0.050252 | NaN | NaN | -0.037456 | NaN | NaN | NaN | NaN | |||||
| 1 | -1 | -1 | NaN | 0.020515 | NaN | NaN | -0.059223 | NaN | NaN | NaN | NaN | NaN | ||||||
| 3 | 1 | -1 | -1 | 1 | 1 | NaN | NaN | NaN | 0.020515 | NaN | NaN | -0.059223 | NaN | NaN | NaN | |||
| 1 | 1 | -1 | NaN | NaN | 0.050252 | NaN | NaN | -0.037456 | NaN | NaN | NaN | NaN | ||||||
| 1 | -1 | -1 | 1 | NaN | NaN | 0.050252 | NaN | NaN | -0.037456 | NaN | NaN | NaN | NaN | |||||
| 1 | -1 | -1 | NaN | 0.020515 | NaN | NaN | -0.059223 | NaN | NaN | NaN | NaN | NaN | ||||||
| 3 | -1 | -1 | 1 | 1 | NaN | NaN | NaN | -0.075872 | NaN | NaN | -0.059734 | NaN | NaN | -0.089473 | ||||
| 1 | 1 | -1 | 0.103893 | NaN | 0.046462 | NaN | NaN | NaN | NaN | NaN | -0.065488 | NaN | ||||||
| 1 | -1 | -1 | 1 | 0.103893 | NaN | 0.046462 | NaN | NaN | NaN | NaN | NaN | -0.065488 | NaN | |||||
| 1 | -1 | -1 | NaN | -0.075872 | NaN | NaN | -0.059734 | NaN | NaN | -0.089473 | NaN | NaN | ||||||
| SU | SG | SU | 1 | 1 | 0 | 0 | 0 | 0 | 2.114595 | NaN | 1.891351 | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 3 | 0 | 0 | 0 | 0 | NaN | NaN | -0.098066 | NaN | NaN | -0.097458 | NaN | NaN | NaN | NaN | ||||
| 3 | 1 | 0 | 0 | 0 | 0 | NaN | NaN | -0.098066 | NaN | NaN | -0.097458 | NaN | NaN | NaN | NaN | |||
| 3 | 0 | 0 | 0 | 0 | 0.186727 | NaN | 0.111343 | NaN | NaN | 0.101851 | NaN | NaN | 0.156936 | NaN | ||||
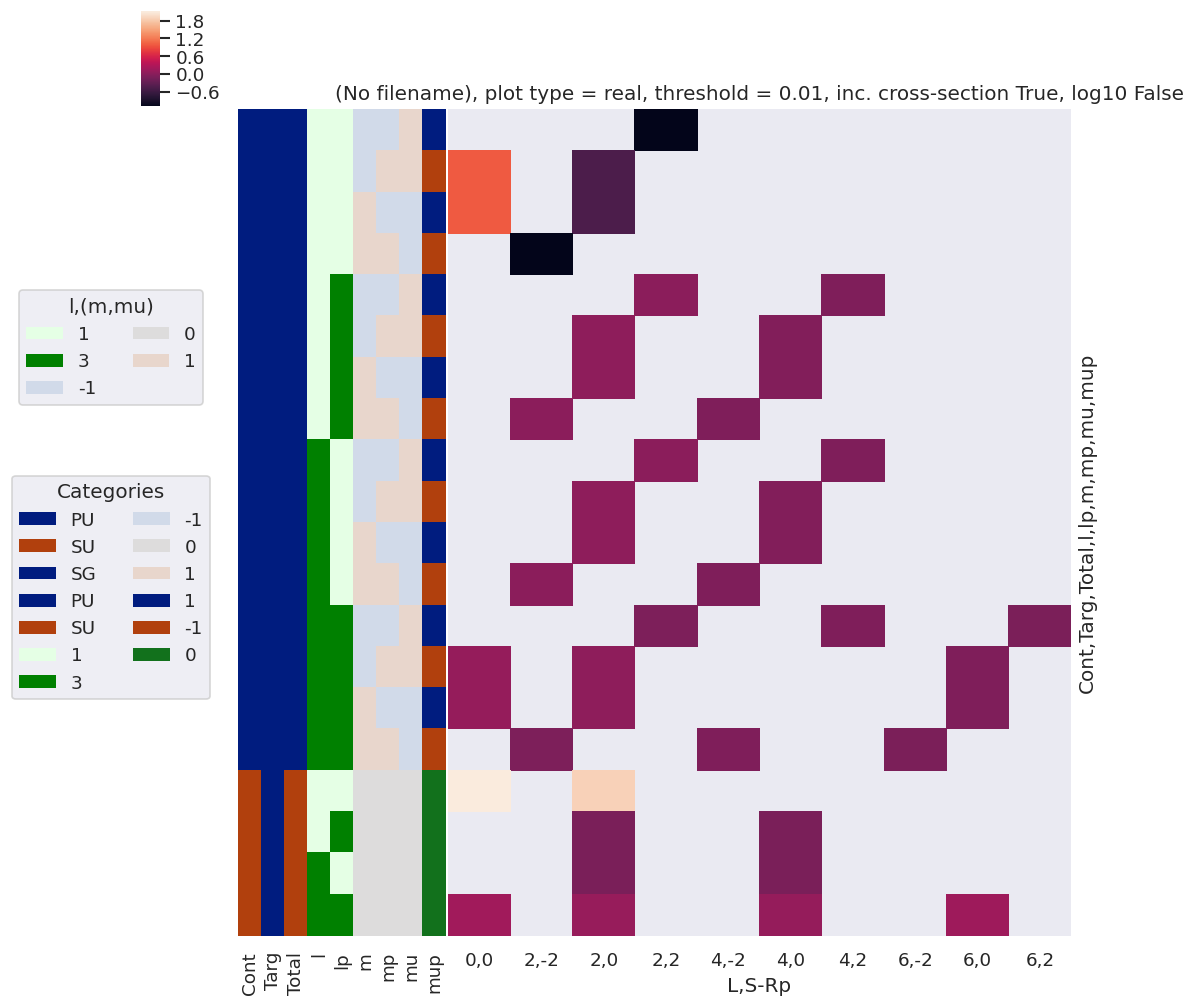
[56]:
xDim = {'LM':['L','M']}
mTermSum = mTerm.sum(sumDims)
mTermSum.attrs['dataType'] = 'matE' # Set matE here to allow for correct plotting of sym dims.
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermSum, xDim='Eke', sumDims=None, pType = 'r', thres = None, fillna = True, SFflag=False)
daPlotpd[0:50]
Plotting data (No filename), pType=r, thres=None, with Seaborn
No handles with labels found to put in legend.
[56]:
| Eke | 0.1 | 1.1 | 2.1 | 3.1 | 4.1 | 5.1 | 6.1 | 7.1 | 8.1 | 9.1 | ... | 41.1 | 42.1 | 43.1 | 44.1 | 45.1 | 46.1 | 47.1 | 48.1 | 49.1 | 50.1 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cont | L | M | S-Rp | Targ | Total | t | |||||||||||||||||||||
| PU | 0 | -1 | -2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| -1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | -2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ||
| -1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | PU | 0 | 0.738022 | 0.720190 | 0.713936 | 0.715632 | 0.723239 | 0.735319 | 0.750596 | 0.767824 | 0.785799 | 0.803414 | ... | 0.389743 | 0.371662 | 0.354243 | 0.337490 | 0.321402 | 0.305977 | 0.291206 | 0.277080 | 0.263586 | 0.250712 | |||
| 1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 1 | -2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ||
| -1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | -1 | -2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |
| -1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | -2 | SG | PU | 0 | 0.185154 | 0.207022 | 0.214972 | 0.218305 | 0.219175 | 0.218591 | 0.217069 | 0.214871 | 0.212125 | 0.208893 | ... | 0.061546 | 0.058851 | 0.056280 | 0.053827 | 0.051487 | 0.049257 | 0.047132 | 0.045107 | 0.043178 | 0.041342 | ||
| -1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | PU | 0 | 0.040253 | 0.091965 | 0.110662 | 0.116569 | 0.114907 | 0.108336 | 0.098461 | 0.086362 | 0.072831 | 0.058489 | ... | -0.051207 | -0.048509 | -0.045862 | -0.043276 | -0.040761 | -0.038323 | -0.035968 | -0.033701 | -0.031523 | -0.029438 | |||
| 1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | PU | 0 | 0.185154 | 0.207022 | 0.214972 | 0.218305 | 0.219175 | 0.218591 | 0.217069 | 0.214871 | 0.212125 | 0.208893 | ... | 0.061546 | 0.058851 | 0.056280 | 0.053827 | 0.051487 | 0.049257 | 0.047132 | 0.045107 | 0.043178 | 0.041342 | |||
| 1 | -2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ||
| -1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 1 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | PU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| SU | 0 | -1 | -2 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| -1 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 1 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | -2 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ||
| -1 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | SU | 0 | 0.767107 | 0.794111 | 0.835793 | 0.889138 | 0.952871 | 1.026468 | 1.109505 | 1.201144 | 1.299572 | 1.401236 | ... | 0.022910 | 0.023531 | 0.024251 | 0.025035 | 0.025854 | 0.026686 | 0.027512 | 0.028319 | 0.029095 | 0.029830 | |||
| 1 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 1 | -2 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ||
| -1 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 1 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | -1 | -2 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |
| -1 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 0 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 1 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | |||
| 2 | SG | SU | 0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
50 rows × 51 columns
[57]:
# mTermSum.XS.real.squeeze().plot.line(x='Eke', col='Sym');
# ep.util.matEleSelector(mTermSum, thres = None, dims='Eke').real.squeeze().plot.line(x='Eke', col='Sym');
ep.util.matEleSelector(mTermSum.sel({'t':0}), thres = 0.01, dims='Eke').real.squeeze().plot.line(x='Eke', row='S-Rp', col='Sym');
[58]:
# mTermSum.XS.real.squeeze().plot.line(x='Eke', col='Sym');
# ep.util.matEleSelector(mTermSum, thres = None, dims='Eke').real.squeeze().plot.line(x='Eke', col='Sym');
ep.util.matEleSelector(mTermSum.sum('S-Rp'), thres = 0.01, dims='Eke').real.squeeze().plot.line(x='Eke', col='Sym');
Testing functional form¶
[59]:
phaseConvention = 'E' # Set phase conventions used in the numerics - for ePolyScat matrix elements, set to 'E', to match defns. above.
symSum = False # Sum over symmetry groups, or keep separate?
SFflag = False # Include scaling factor to Mb in calculation?
thres = 1e-4
RX = ep.setPolGeoms() # Set default pol geoms (z,x,y), or will be set by mfblmXprod() defaults - FOR AF case this is only used to set 'z' geom for unity wigner D's - should rationalise this!
start = time.time()
mTermST, mTermS, mTermTest, BetaNormX = ep.geomFunc.afblmXprod(dataSet[0], QNs = None, RX=RX, thres = thres, selDims = {'it':1, 'Type':'L'}, thresDims='Eke', symSum=symSum, phaseConvention=phaseConvention,
SFflag=False, SFflagRenorm = False, BLMRenorm = 1,sumDims = ['mu', 'mup', 'l','lp','m','mp','S-Rp'])
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points, {2} polarizations, threshold={3}.'.format((end-start), mTermST.Eke.size, RX.size, thres))
# Elapsed time = 3.3885273933410645 seconds, for 51 energy points, 3 polarizations, threshold=0.01.
# Elapsed time = 5.059587478637695 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
Elapsed time = 2.4853365421295166 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
[60]:
# Full results (before summation)
mTermST.attrs['dataType'] = 'matE' # Set matE here to allow for correct plotting of sym dims.
plotDimsRed = ['Labels','L','M'] # Set plotDims to fix dim ordering in plot
if not symSum:
plotDimsRed.extend(['Cont','Targ','Total'])
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, plotDims=plotDimsRed, xDim='Eke', sumDims=None, pType = 'r', thres = None, fillna = True, SFflag=False)
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True) # If plotDims is not passed use default ordering.
Plotting data n2_3sg_0.1-50.1eV_A2.inp.out, pType=r, thres=None, with Seaborn
No handles with labels found to put in legend.
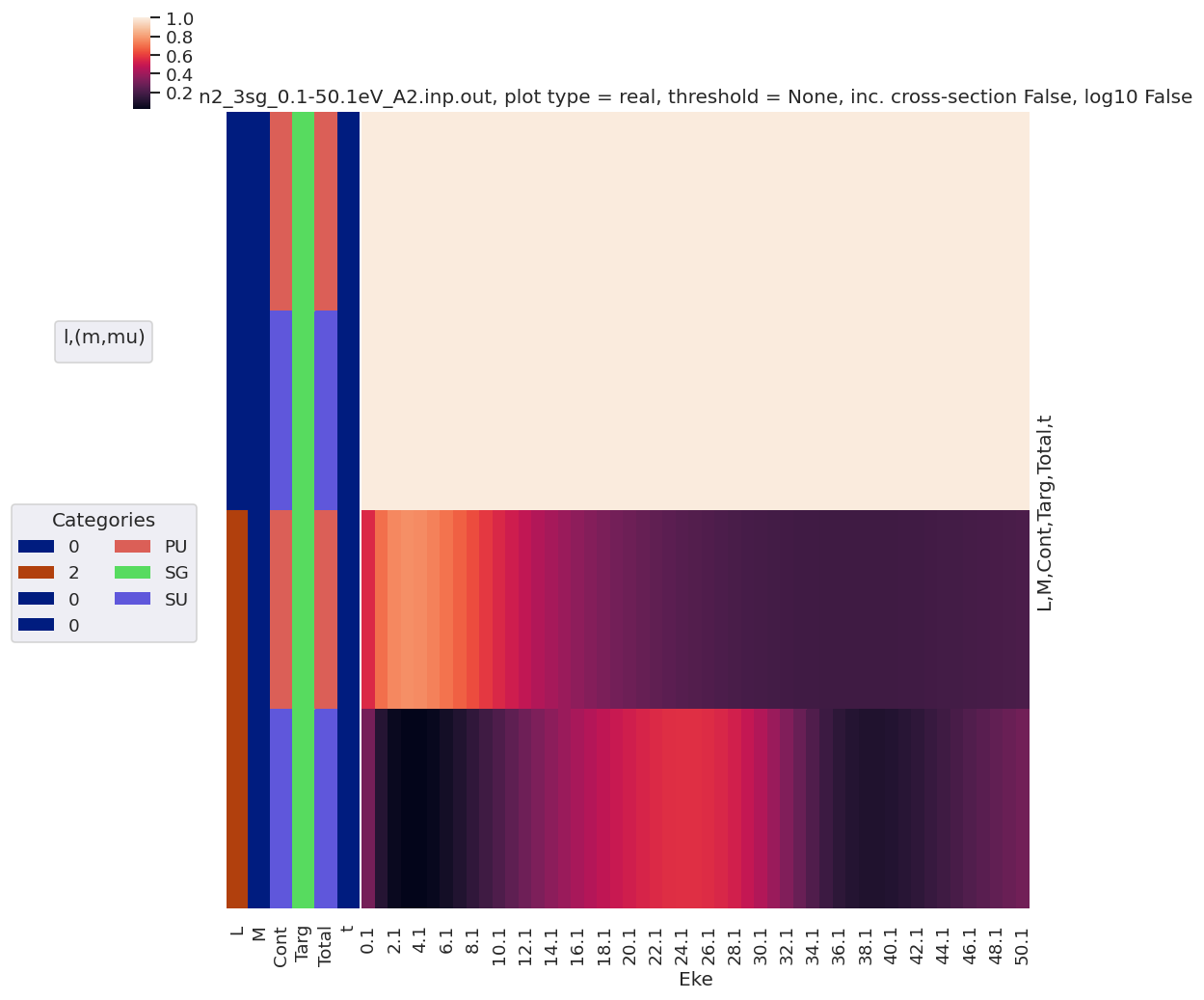
[61]:
mTermST.XSraw.real.squeeze().plot.line(x='Eke', col='Sym');
(mTermST.XSrescaled).real.squeeze().plot.line(x='Eke', col='Sym');
(mTermST.XSiso).real.squeeze().plot.line(x='Eke', col='Sym');
[62]:
# Plot cross sections using Xarray functionality
dataXS[0].sel({'Type':'L', 'XC':'SIGMA'}).plot.line(x='Eke');
# (2*mTermST.XSrescaled).real.squeeze().plot.line(x='Eke', linestyle='dashed');
(mTermST.XSrescaled).pipe(np.abs).squeeze().plot.line(x='Eke', linestyle='dashed');
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\plot\plot.py:86: FutureWarning:
This DataArray contains multi-dimensional coordinates. In the future, these coordinates will be transposed as well unless you specify transpose_coords=False.
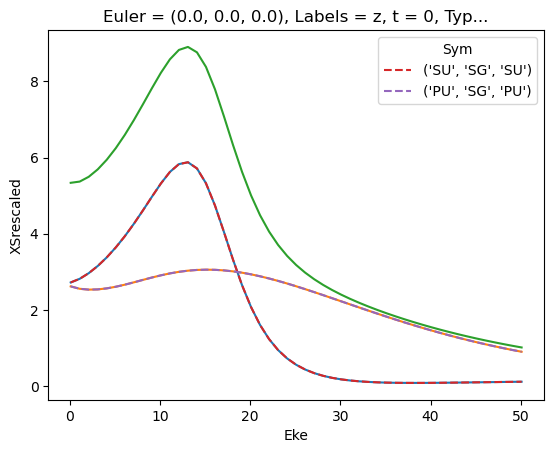
[63]:
# Test normalisation as per CG version (see lfblmGeom.py) - NOW SET IN FUNCTION
# XSmatE = (matEthres * matEthres.conj()).sum(['LM','mu']) # Use selected & thresholded matE.
# # NOTE - this may fail in current form if dims are missing.
# normBeta = 3/5 * (1/XSmatE) # Normalise by sum over matrix elements squared.
# normBeta.sel({'Cont':'PU'}).real.plot.line(x='Eke')
# ep.util.matEleSelector(mTermST*normBeta, thres = None, dims='Eke').real.squeeze().plot.line(x='Eke', col='Sym');
[64]:
# Try converting to BL values...
BLvals = ep.util.conversion.conv_BL_BLM(mTermST, to='lg')
ep.util.matEleSelector(BLvals, thres = None, dims='Eke').real.squeeze().plot.line(x='Eke', col='Sym');
plt.figure();
dataXS[0].sel({'Type':'L', 'XC':'BETA'}).plot.line(x='Eke', linestyle = 'dashed'); # Ref. values from GetCro
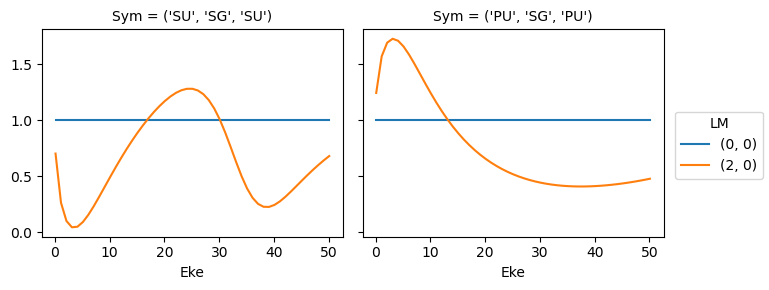
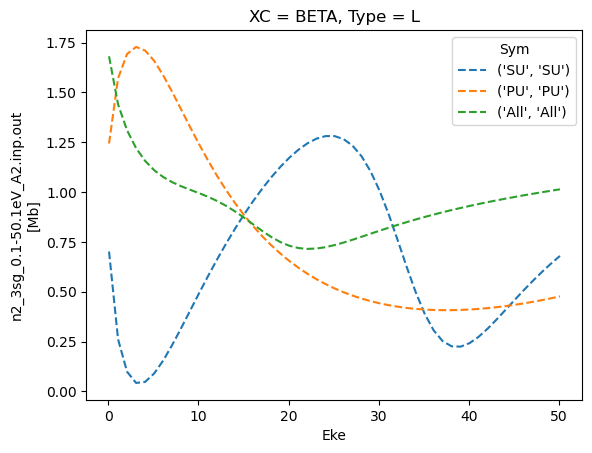
[65]:
(BLvals.XSrescaled).pipe(np.abs).squeeze().plot.line(x='Eke', linestyle='dashed');
C:\Users\femtolab\.conda\envs\ePSdev\lib\site-packages\xarray\plot\plot.py:86: FutureWarning:
This DataArray contains multi-dimensional coordinates. In the future, these coordinates will be transposed as well unless you specify transpose_coords=False.
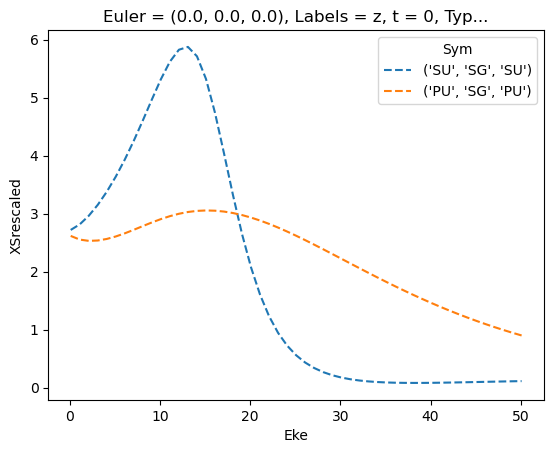
Try sym summation…¶
[66]:
phaseConvention = 'E' # Set phase conventions used in the numerics - for ePolyScat matrix elements, set to 'E', to match defns. above.
symSum = True # Sum over symmetry groups, or keep separate?
SFflag = False # Include scaling factor to Mb in calculation?
thres = 1e-4
RX = ep.setPolGeoms() # Set default pol geoms (z,x,y), or will be set by mfblmXprod() defaults - FOR AF case this is only used to set 'z' geom for unity wigner D's - should rationalise this!
start = time.time()
mTermST, mTermS, mTermTest, BetaNormX = ep.geomFunc.afblmXprod(dataSet[0], QNs = None, RX=RX, thres = thres, selDims = {'it':1, 'Type':'L'}, thresDims='Eke', symSum=symSum, SFflag=SFflag, phaseConvention=phaseConvention)
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points, {2} polarizations, threshold={3}.'.format((end-start), mTermST.Eke.size, RX.size, thres))
# Elapsed time = 3.3885273933410645 seconds, for 51 energy points, 3 polarizations, threshold=0.01.
# Elapsed time = 5.059587478637695 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
Elapsed time = 2.3291077613830566 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
[67]:
# Full results (before summation)
mTermST.attrs['dataType'] = 'matE' # Set matE here to allow for correct plotting of sym dims.
plotDimsRed = ['Labels','L','M'] # Set plotDims to fix dim ordering in plot
if not symSum:
plotDimsRed.extend(['Cont','Targ','Total'])
daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, plotDims=plotDimsRed, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True, SFflag=False)
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True) # If plotDims is not passed use default ordering.
Plotting data n2_3sg_0.1-50.1eV_A2.inp.out, pType=r, thres=0.01, with Seaborn
No handles with labels found to put in legend.
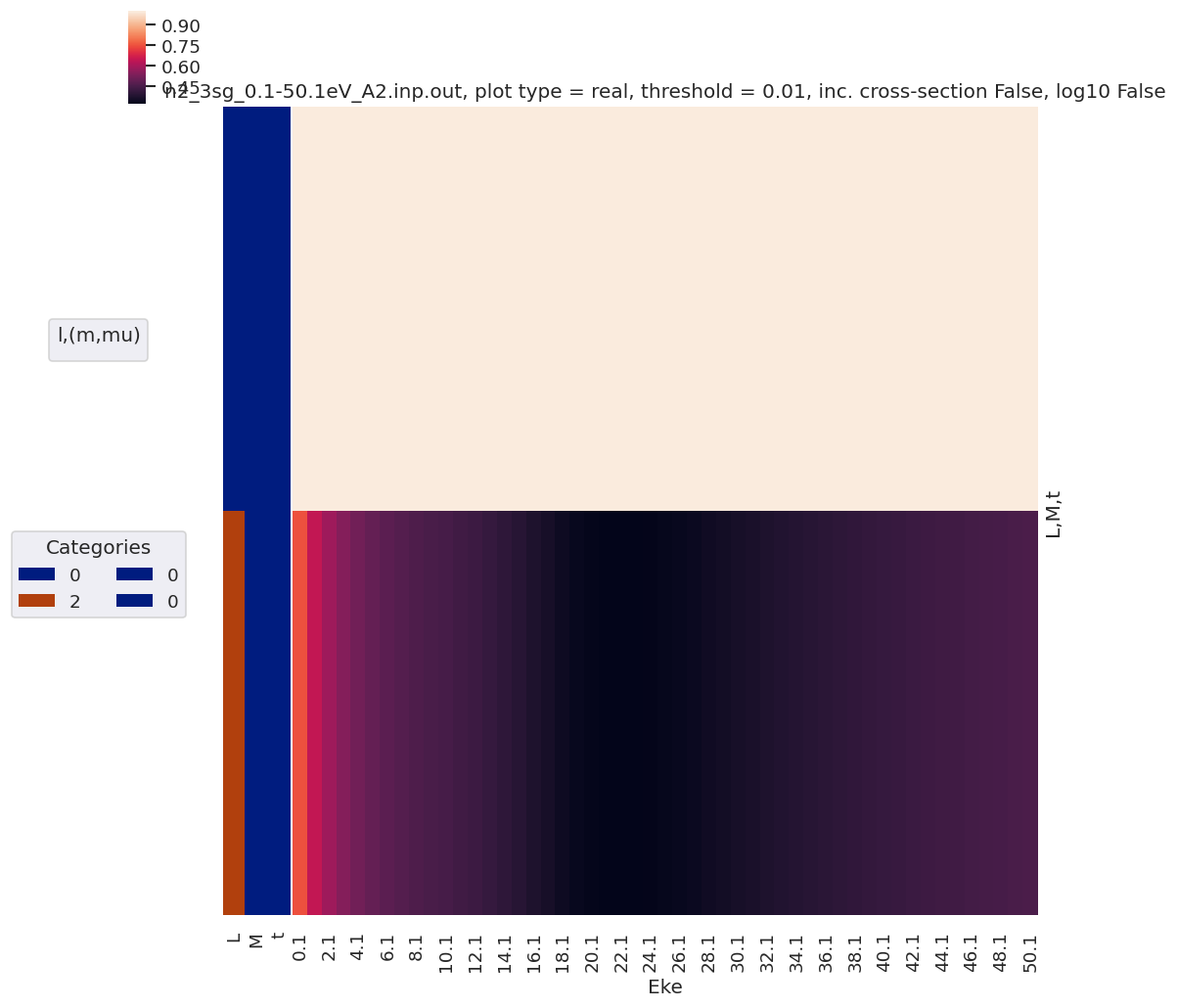
[68]:
mTermST.XSraw.real.squeeze().plot.line(x='Eke');
mTermST.XSrescaled.real.squeeze().plot.line(x='Eke');
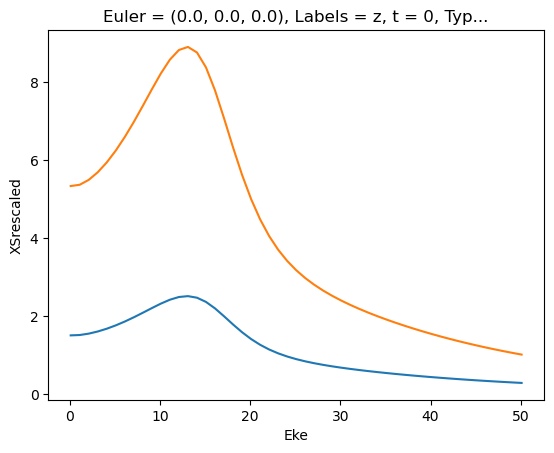
[69]:
# 09/09/20 - updating here for BetaNormX values...
plotThres = 1e-2
ep.util.matEleSelector(BetaNormX['XSraw'], thres = plotThres, dims='Eke', sq=True, drop=True).real.plot.line(x='Eke'); # Values from AF code - note these are small, with complex terms
ep.util.matEleSelector(BetaNormX['XSrescaled'], thres = plotThres, dims='Eke', sq=True, drop=True).real.plot.line(x='Eke'); # Values from AF code - real valued
ep.util.matEleSelector(BetaNormX['XSiso'], thres = plotThres, dims='Eke', sq=True, drop=True).real.plot.line(x='Eke'); # Values from sum over matrix elements
# Ref. values from LF code
# ep.util.matEleSelector(BetaNormX_sph['XS'], thres = plotThres, dims='Eke', sq=True, drop=True).real.plot.line(x='Eke', linestyle='dashed'); # Values from LF code.
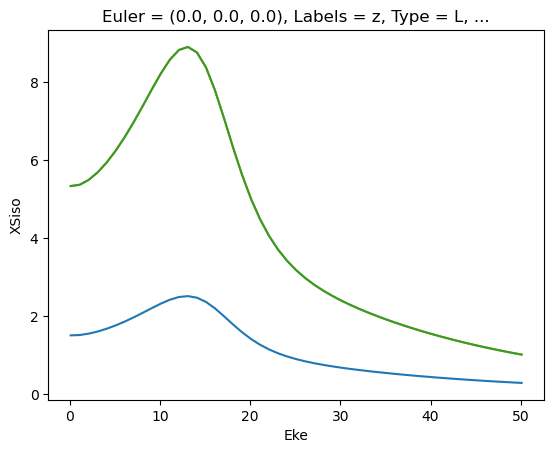
[70]:
ep.util.matEleSelector(mTermST, thres = 0.1, dims='Eke').real.squeeze().plot.line(x='Eke');
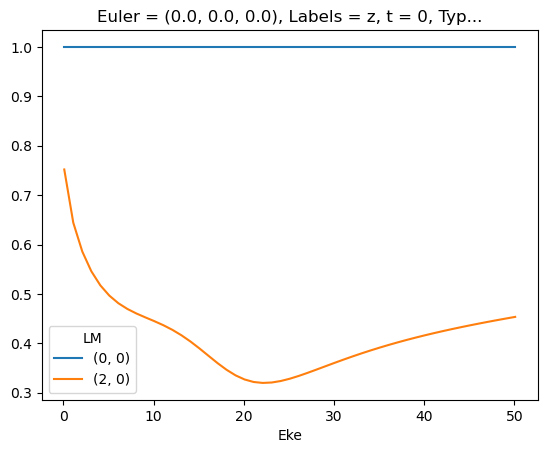
First attempt… with sym summation
- Looks quite different - might be SF issue with combining continua, and/or degen factor…?
- Looks same as previous AF code attempt (http://localhost:8888/lab/tree/dev/ePSproc/ePSproc_AFBLM_calcs_bench_100220.ipynb), suggesting something in degen/normalisation in formalism amiss?
EDIT 10/09/20: now fixed, issues with normalisation and Spherical Harmonic and Legendre function defintions - see LF/AF test notebook for details
[71]:
# ep.util.matEleSelector(mTermST, thres = 0.1, dims='Eke').real.squeeze().plot.line(x='Eke');
ep.util.matEleSelector(mTermST, thres = 0.1, dims='Eke').imag.squeeze().plot.line(x='Eke');
Test compared to experimental N2 AF results…¶
In this case MF PADs look good, so also expect good agreement with AF…
[72]:
# Adapted from ePSproc_AFBLM_testing_010519_300719.m
# Load ADMs for N2
from scipy.io import loadmat
ADMdataFile = os.path.join(modPath, 'data', 'alignment', 'N2_ADM_VM_290816.mat')
ADMs = loadmat(ADMdataFile)
[73]:
# Set tOffset for calcs, 3.76ps!!!
# This is because this is 2-pulse case, and will set t=0 to 2nd pulse (and matches defn. in N2 experimental paper)
tOffset = -3.76
ADMs['time'] = ADMs['time'] + tOffset
[74]:
# Plot
import matplotlib.pyplot as plt
plt.plot(ADMs['time'].T, np.real(ADMs['ADM'].T))
plt.legend(ADMs['ADMlist'])
plt.xlabel('t/ps')
plt.ylabel('ADM')
plt.show()
[74]:
[<matplotlib.lines.Line2D at 0x1da183b19e8>,
<matplotlib.lines.Line2D at 0x1da183b17f0>,
<matplotlib.lines.Line2D at 0x1da183b12e8>,
<matplotlib.lines.Line2D at 0x1da183b1668>]
[74]:
<matplotlib.legend.Legend at 0x1da1838a1d0>
[74]:
Text(0.5, 0, 't/ps')
[74]:
Text(0, 0.5, 'ADM')
[75]:
# Selection & downsampling
trange=[1, 9.5] # Set range in ps for calc
tStep=5 # Set tStep for downsampling
tMask = (ADMs['time']>trange[0]) * (ADMs['time']<trange[1])
ind = np.nonzero(tMask)[1][0::tStep]
At = ADMs['time'][:,ind].squeeze()
ADMin = ADMs['ADM'][:,ind]
print(f"Selecting {ind.size} points")
plt.plot(At, np.real(ADMin.T))
plt.legend(ADMs['ADMlist'])
plt.xlabel('t/ps')
plt.ylabel('ADM')
plt.show()
# Set in Xarray
ADMX = ep.setADMs(ADMs = ADMs['ADM'][:,ind], t=At, KQSLabels = ADMs['ADMlist'], addS = True)
# ADMX
Selecting 87 points
[75]:
[<matplotlib.lines.Line2D at 0x1da19862518>,
<matplotlib.lines.Line2D at 0x1da198622b0>,
<matplotlib.lines.Line2D at 0x1da19862828>,
<matplotlib.lines.Line2D at 0x1da19862748>]
[75]:
<matplotlib.legend.Legend at 0x1da19eb1630>
[75]:
Text(0.5, 0, 't/ps')
[75]:
Text(0, 0.5, 'ADM')
[76]:
# Run with sym summation...
phaseConvention = 'E' # Set phase conventions used in the numerics - for ePolyScat matrix elements, set to 'E', to match defns. above.
symSum = True # Sum over symmetry groups, or keep separate?
SFflag = False # Include scaling factor to Mb in calculation?
SFflagRenorm = False # Renorm terms
BLMRenorm = 1
thres = 1e-4
RX = ep.setPolGeoms() # Set default pol geoms (z,x,y), or will be set by mfblmXprod() defaults - FOR AF case this is only used to set 'z' geom for unity wigner D's - should rationalise this!
start = time.time()
mTermST, mTermS, mTermTest, BetaNormX = ep.geomFunc.afblmXprod(dataSet[0], QNs = None, AKQS=ADMX, RX=RX, thres = thres, selDims = {'it':1, 'Type':'L'}, thresDims='Eke',
symSum=symSum, SFflag=SFflag, BLMRenorm = BLMRenorm,
phaseConvention=phaseConvention)
end = time.time()
print('Elapsed time = {0} seconds, for {1} energy points, {2} polarizations, threshold={3}.'.format((end-start), mTermST.Eke.size, RX.size, thres))
# Elapsed time = 3.3885273933410645 seconds, for 51 energy points, 3 polarizations, threshold=0.01.
# Elapsed time = 5.059587478637695 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
Elapsed time = 6.940988779067993 seconds, for 51 energy points, 3 polarizations, threshold=0.0001.
[77]:
# Full results (before summation)
mTermST.attrs['dataType'] = 'matE' # Set matE here to allow for correct plotting of sym dims.
plotDimsRed = ['Labels','L','M'] # Set plotDims to fix dim ordering in plot
if not symSum:
plotDimsRed.extend(['Cont','Targ','Total'])
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, plotDims=plotDimsRed, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True, SFflag=False)
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True) # If plotDims is not passed use default ordering.
[78]:
# daPlot, daPlotpd, legendList, gFig = ep.lmPlot(mTermST.XS, plotDims=plotDimsRed, xDim='Eke', sumDims=None, pType = 'r', thres = 0.01, fillna = True, SFflag=False)
[79]:
mTermST.XSrescaled.real.plot()
mTermST.where(mTermST.L > 0).real.plot(col='LM')
[79]:
<matplotlib.collections.QuadMesh at 0x1da190f54a8>
[79]:
<xarray.plot.facetgrid.FacetGrid at 0x1da1cfca048>
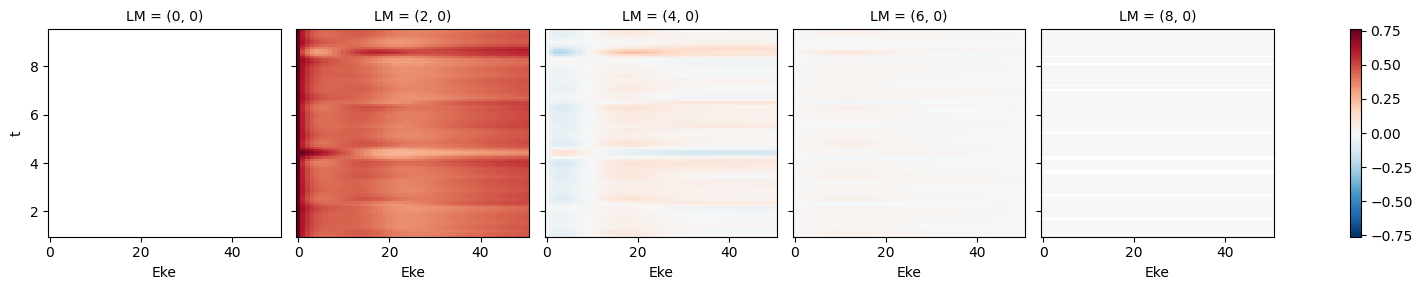
[80]:
# Plot single energy XS
E = 8.1
mTermST.XSraw.sel({'Eke':E}).real.squeeze().plot.line(x='t');
# mTermST.XSrescaled.sel({'Eke':E}).real.squeeze().plot.line(x='t');
[81]:
# LM with renorm
mTermST.sel({'Eke':E}).where(mTermST['L']>0).real.squeeze().plot.line(x='t');
# Lineshapes look good, but abs. values are low compared to expt. (see below)
[82]:
# # With further renorm by B00(t), BLMRenorm =2 or 3
# # This looks pretty good for shape... but about x2 lower than ref. experimental values????
# # 01/09/20: now looking a bit better with updated renorm routine (BLMRenorm =3 case)
# print(BLMRenorm)
# ep.util.matEleSelector(mTermST, thres = 1e-4, dims='t').sel({'Eke':E}).real.squeeze().plot.line(x='t');
# plt.figure()
# # ep.util.matEleSelector((mTermST/mTermST.XS), thres = 1e-4, dims='t').sel({'Eke':E}).where(mTermST.L > 0).real.squeeze().plot.line(x='t');
# ep.util.matEleSelector((mTermST/mTermST.XSraw), thres = 1e-4, dims='t').sel({'Eke':E}).real.squeeze().plot.line(x='t');
# ep.util.matEleSelector((mTermST/mTermST.XS), thres = 1e-4, dims='t').sel({'Eke':E}).pipe(np.abs).squeeze().plot.line(x='t', linestyle="dashed");
# plt.figure()
# ep.util.matEleSelector(mTermST/mTermST.sel({'L':0,'M':0}), thres = 1e-4, dims='t').sel({'Eke':E}).real.squeeze().plot.line(x='t');
[83]:
# Check Lg converted values... does this fix possible magnitude issue?
ep.util.matEleSelector(ep.conversion.conv_BL_BLM(mTermST, to='lg'), thres = 1e-6, dims='t').sel({'Eke':E}).where(mTermST['L']>0).real.squeeze().plot.line(x='t');
# ep.util.matEleSelector(ep.conversion.conv_BL_BLM(mTermST/mTermST.sel({'L':0,'M':0}), to='lg'), thres = 1e-6, dims='t').sel({'Eke':E}).where(mTermST['L']>0).real.squeeze().plot.line(x='t');
01/09/20: FEELS like progress, but still not quite correct - values a bit small (Sph), or a bit large (Lg) - might be an issue with experimental renorm, since B00 ~ 1.2?
Experimental results¶
(Fig 2 from Marceau, Claude, Varun Makhija, Dominique Platzer, A. Yu. Naumov, P. B. Corkum, Albert Stolow, D. M. Villeneuve, and Paul Hockett. “Molecular Frame Reconstruction Using Time-Domain Photoionization Interferometry.” Physical Review Letters 119, no. 8 (August 2017): 083401. https://doi.org/10.1103/PhysRevLett.119.083401. Full data at https://doi.org/10.6084/m9.figshare.4480349.v10)
Currently:
- Relative signs/phases of betas look good at 4.1eV… but not at 7.1 or 8.1eV! (Experimental MFPAD comparison energy) - suggests still phase and/or renorm issue somewhere?
- Values still off, same issue probably.
- Might be phase issue with sum over rotation matrix elements, which are conj() in MF case, but not in original derivation here…? This could give 3j sign-flip, hence change calculated alignment response.
UPDATE 07/07/20 (after LF testing and degen partial fix):
- Now looking reasonable at 7.1eV by shape, but off at 8.1eV (i.e. transition zone has shifted up in E).
- Still have some issue(s) with abs. values, and XS vs. E. This is the case if SF is included, and also if not!
Version info¶
[84]:
import scooby
scooby.Report(additional=['epsproc', 'xarray', 'holoviews'])
[84]:
| Thu Sep 10 18:31:17 2020 Eastern Daylight Time | |||||
| OS | Windows | CPU(s) | 32 | Machine | AMD64 |
| Architecture | 64bit | RAM | 63.9 GB | Environment | Jupyter |
| Python 3.7.3 (default, Apr 24 2019, 15:29:51) [MSC v.1915 64 bit (AMD64)] | |||||
| epsproc | 1.2.5-dev | xarray | 0.15.0 | holoviews | 1.13.3 |
| numpy | 1.19.1 | scipy | 1.3.0 | IPython | 7.12.0 |
| matplotlib | 3.3.1 | scooby | 0.5.6 | ||
| Intel(R) Math Kernel Library Version 2020.0.0 Product Build 20191125 for Intel(R) 64 architecture applications | |||||